Question: Show the work (1 point) Note: The notation from this problem is from Understanding Cryptography by Paar and Pelzi. Suppose you have an LFSR with
Show the work
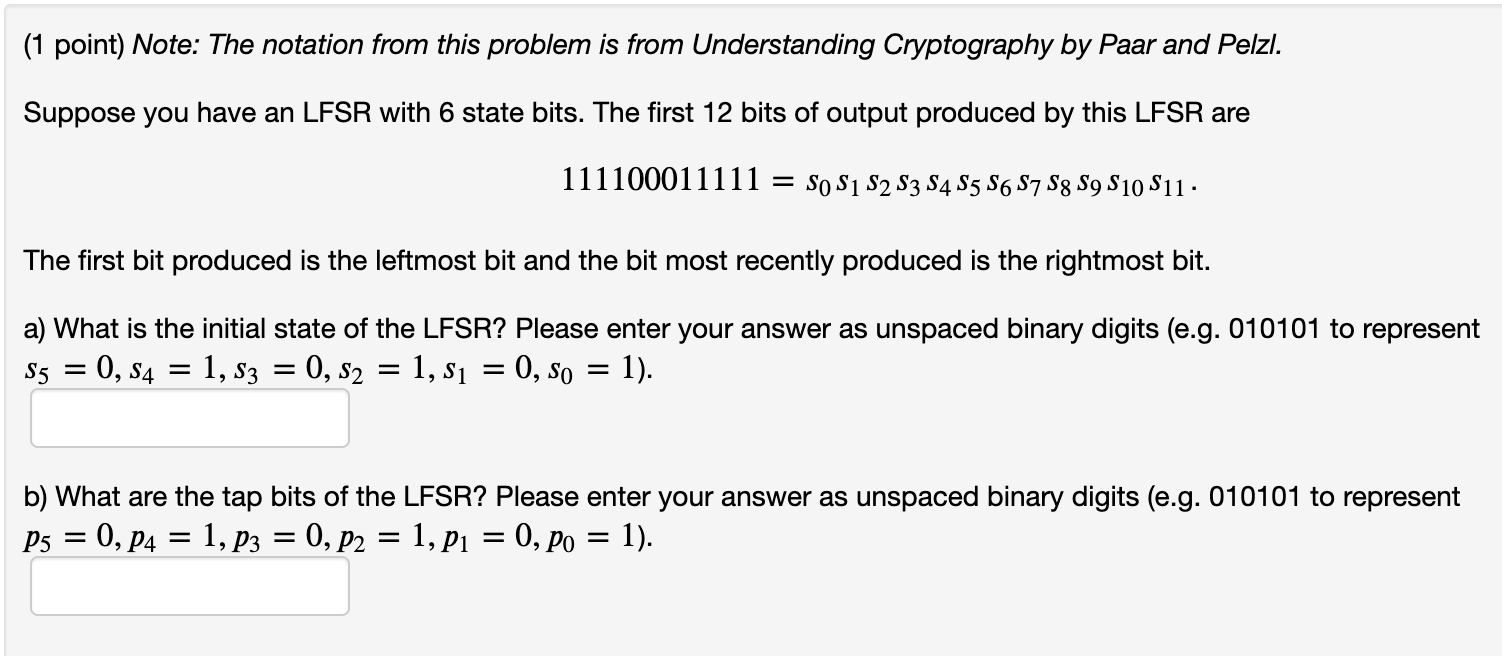

(1 point) Note: The notation from this problem is from Understanding Cryptography by Paar and Pelzi. Suppose you have an LFSR with 6 state bits. The first 12 bits of output produced by this LFSR are 111100011111 = so S1 S2 S3 S4 S5 S6 S7 S8 S9 S10 S11 The first bit produced is the leftmost bit and the bit most recently produced is the rightmost bit. a) What is the initial state of the LFSR? Please enter your answer as unspaced binary digits (e.g. 010101 to represent S5 = 0, $4 = 1, S3 0, S2 = 1, s = 0, SO 1). = = b) What are the tap bits of the LFSR? Please enter your answer as unspaced binary digits (e.g. 010101 to represent P5 = 0, P4 = 1, P3 = 0, P2 = 1, P1 = 0, po = 1). (1 point) Note: The notation from this problem is from Understanding Cryptography by Paar and Pelzi. Consider the LFSR represented by the polynomial x4 + x3 + x + 1. What are the tap bits of the LFSR? Please enter your answer as unspaced binary digits (e.g. 010101 to represent P5 = 0,24 = 1, P3 = 0, P2 = 1, P1 = 0, po = 1). (1 point) Note: The notation from this problem is from Understanding Cryptography by Paar and Pelzi. Suppose you have an LFSR with 6 state bits. The first 12 bits of output produced by this LFSR are 111100011111 = so S1 S2 S3 S4 S5 S6 S7 S8 S9 S10 S11 The first bit produced is the leftmost bit and the bit most recently produced is the rightmost bit. a) What is the initial state of the LFSR? Please enter your answer as unspaced binary digits (e.g. 010101 to represent S5 = 0, $4 = 1, S3 0, S2 = 1, s = 0, SO 1). = = b) What are the tap bits of the LFSR? Please enter your answer as unspaced binary digits (e.g. 010101 to represent P5 = 0, P4 = 1, P3 = 0, P2 = 1, P1 = 0, po = 1). (1 point) Note: The notation from this problem is from Understanding Cryptography by Paar and Pelzi. Consider the LFSR represented by the polynomial x4 + x3 + x + 1. What are the tap bits of the LFSR? Please enter your answer as unspaced binary digits (e.g. 010101 to represent P5 = 0,24 = 1, P3 = 0, P2 = 1, P1 = 0, po = 1)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


