Show your work.

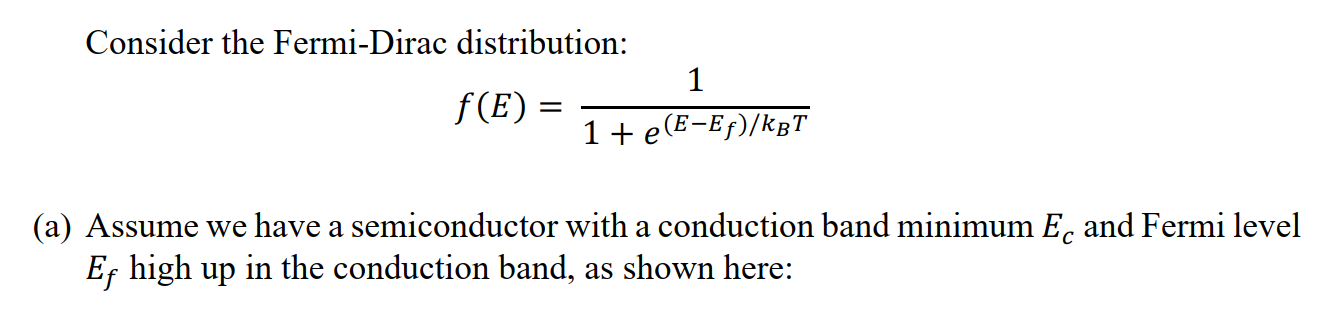
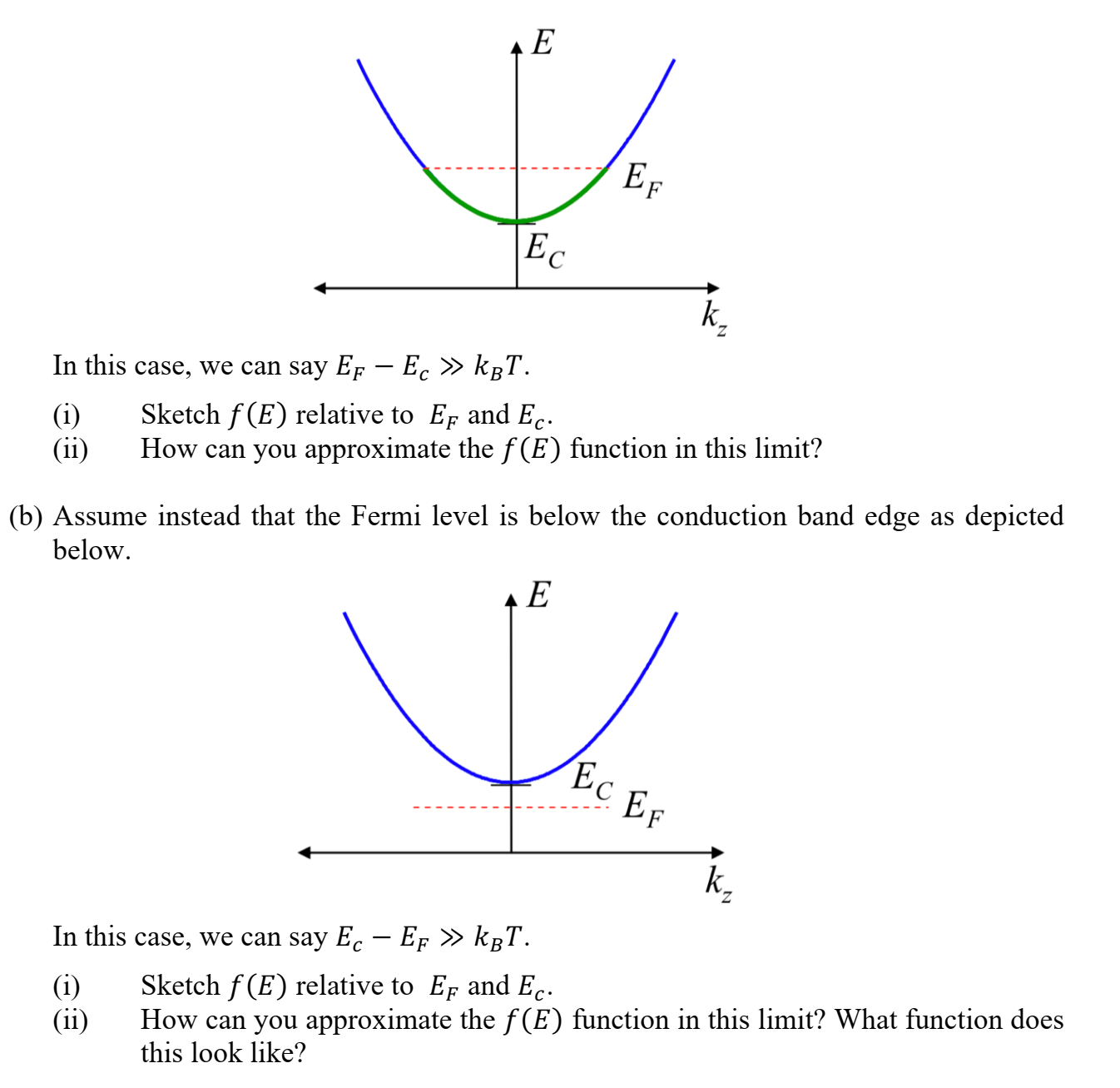
Consider the Fermi-Dirac distribution: f (E) = 1 + e(E-Ef ) / KBT (a) Assume we have a semiconductor with a conduction band minimum E and Fermi level Ef high up in the conduction band, as shown here:In this case, we can say 13,: EC >> kBT. (i) Sketch f (E ) relative to E F and EC. (ii) How can you approximate the f (E) function in this limit? (b) Assume instead that the Fermi level is below the conduction band edge as depicted below. E In this case, we can say EC EF >> kBT. (i) Sketch f (E) relative to E F and EC. (ii) How can you approximate the f (E) function in this limit? What function does this look like