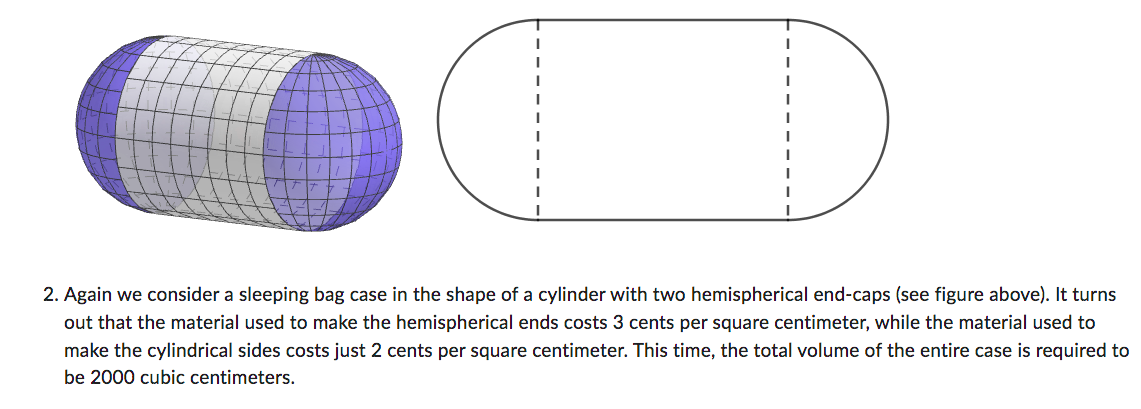
Solve both of the problems below. Show all your work, and clearly indicate your answers, including units. Be sure to explain how you know that the value that you have found is actually the minimum or maximum (as appropriate). When you are finished, scan or take pictures of your written work and upload it for grading. 1. A sleeping bag case is to be manufactured in the shape of a cylinder with two hemispherical end-caps (see figure below). The total surface area is to be 400 square centimeters. a. Write an equation expressing the length of the cylinder, L, in terms of its radius,. b. Write a formula for V(r), the volume of the cylindrical portion of the case, expressed as a function off (and only ; the letter L should not appear in your solution). c. What is the domain of your function V(r)? d. Find the value of r that maximizes V(r) on your domain. e. Interpret your result: what dimensions would maximize the volume, and what would the maximum volume be? D 2. Again we consider a sleeping bag case in the shape of a cylinder with two hemispherical end-caps (see figure above). It turns out that the material used to make the hemispherical ends costs 3 cents per square centimeter, while the material used to make the cylindrical sides costs just 2 cents per square centimeter. This time, the total volume of the entire case is required to be 2000 cubic centimeters. a. Write an equation expressing the length of the cylinder, L, in terms of its radius, 7. b. Write a formula for C(r), the cost of materials for the case, expressed as a function off (and only r; the letter should not appear in your solution). c. What is the domain of your function C(r)? d. Find the value of r that minimizesC(r) on your domain. e. Interpret your result: what dimensions would minimize the cost, and what would the minimum cost be?