Question: solve in excel then type answer please A hair salon in a crowded city anticipates a demand of 30 customers per hour (Poisson arrivals), and
solve in excel then type answer please
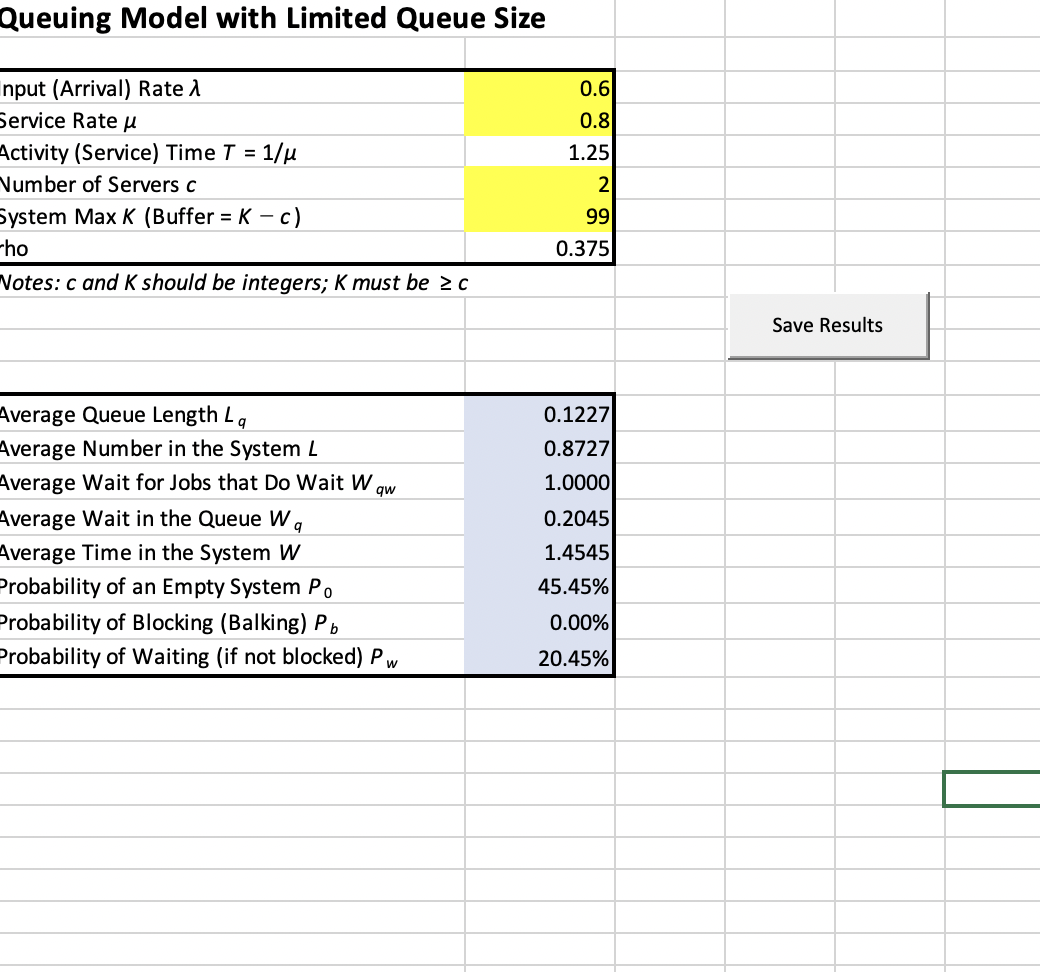
A hair salon in a crowded city anticipates a demand of 30 customers per hour (Poisson arrivals), and it can serve 45 customers per hour (exponentially distributed). The salon is very crowded, so the manager wants to minimize the number of seats needed for waiting customers. At the same time, she doesnt want to lose too many customers who would leave when all waiting seats are occupied. Compute the fewest waiting seats that can be placed in the salon such that the probability of a customer balking and not entering the salon is less
What values should i insert to table to solve? than 2.0% 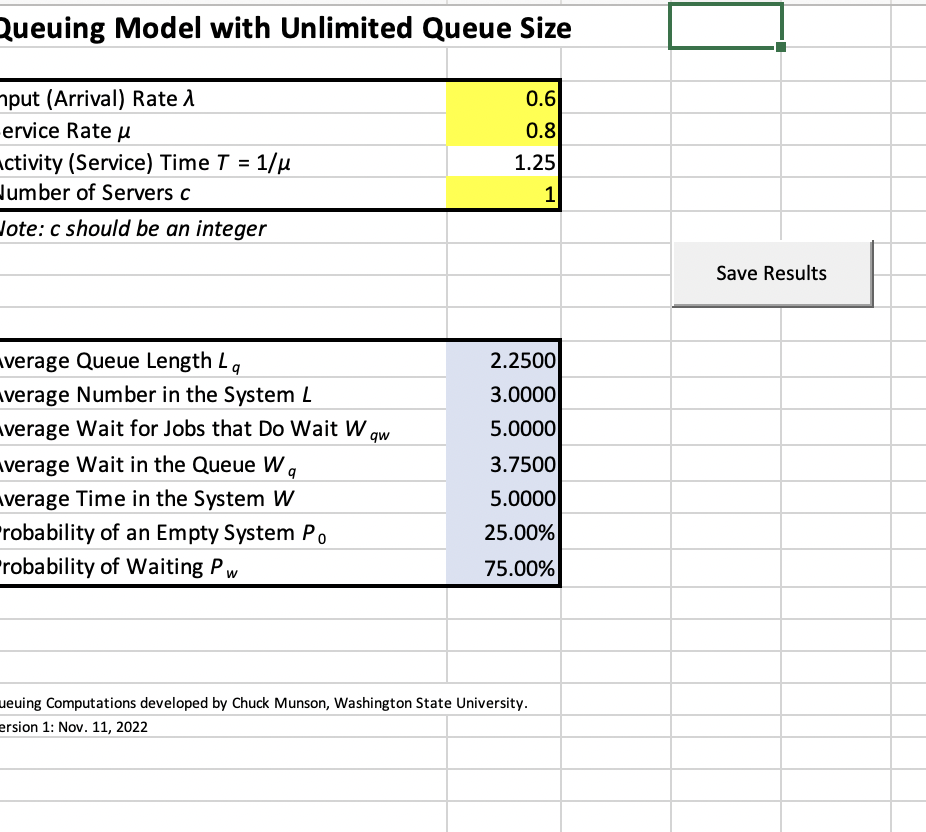
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


