Solve in excel what values should i put in? I need to just submit the tables of results on the last photo, thank you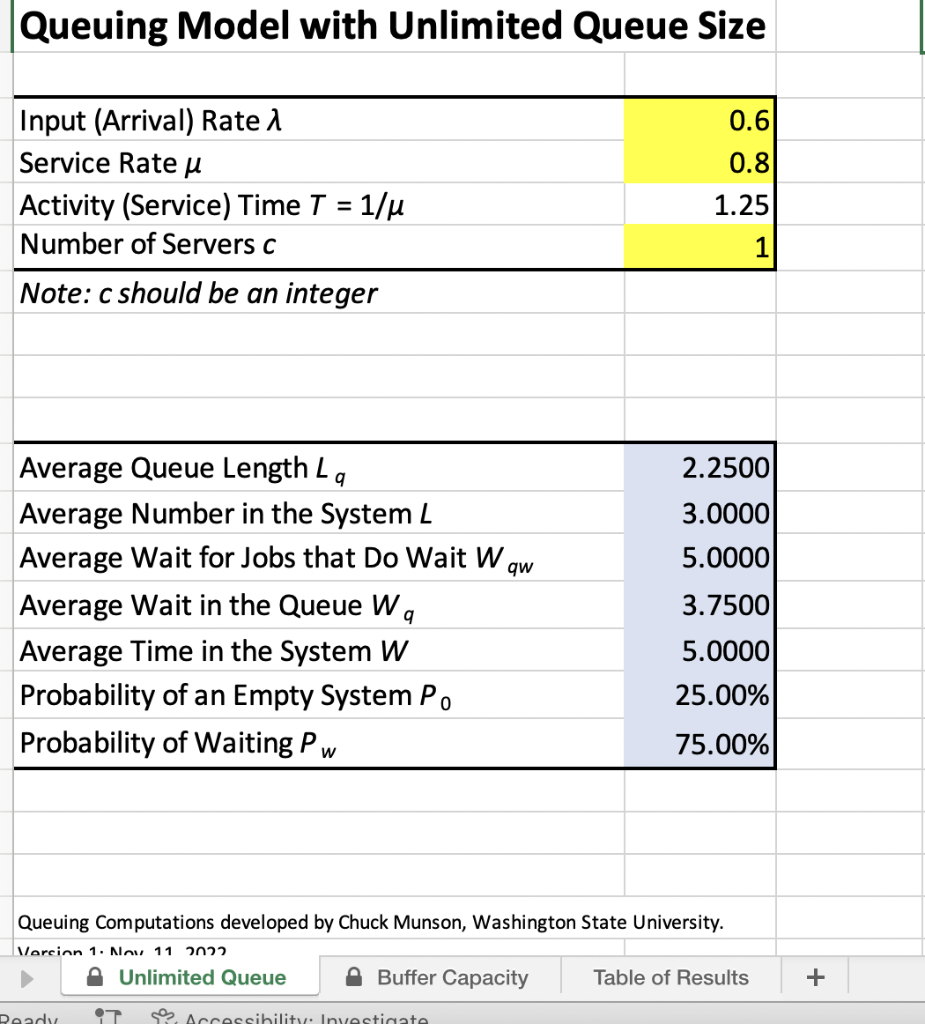

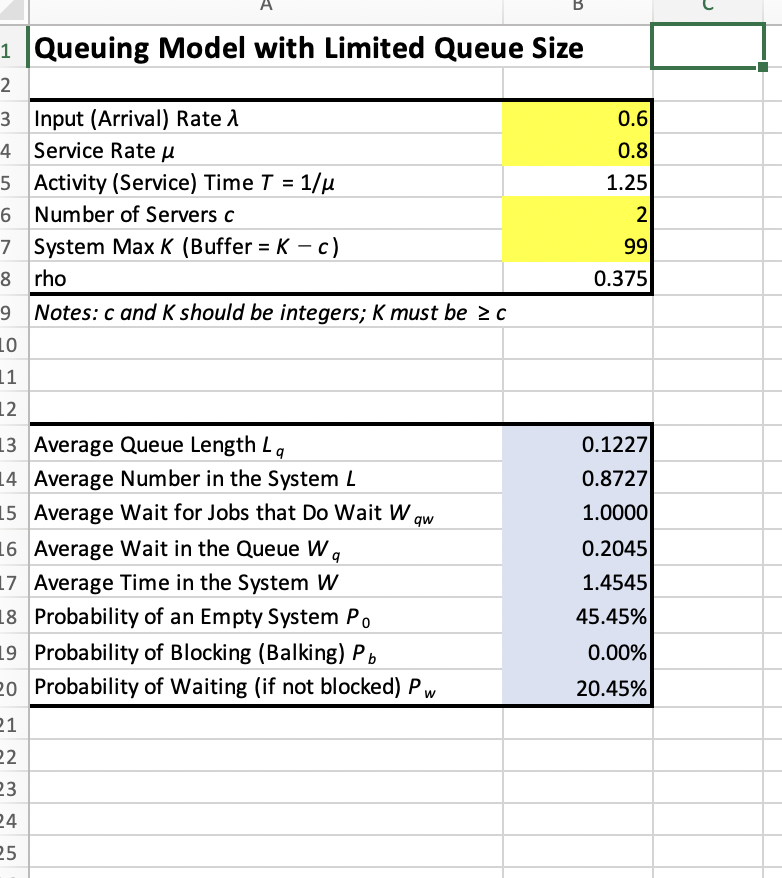
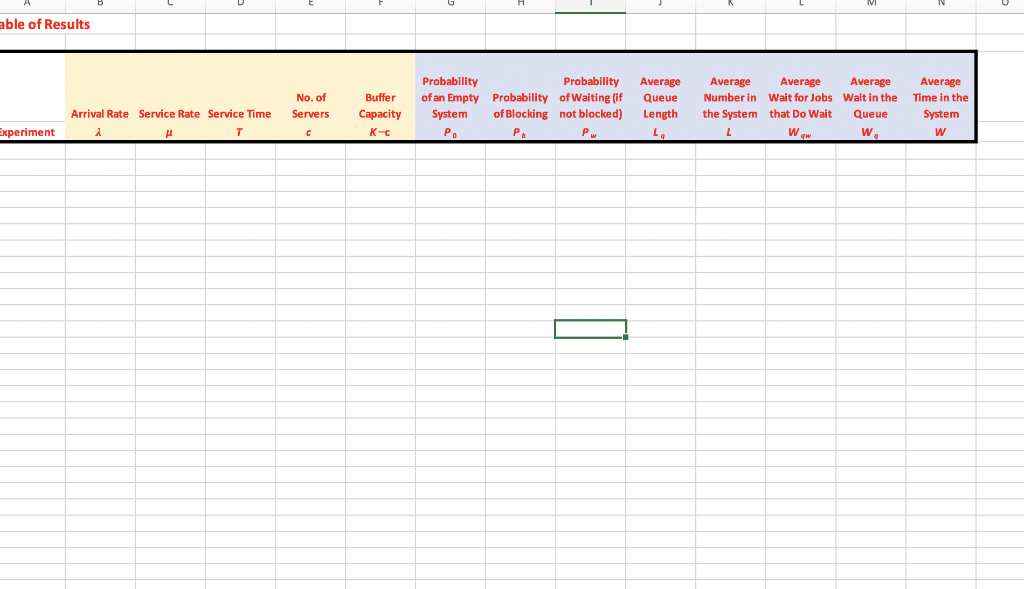
A hair salon in a crowded city anticipates a demand of 30 customers per hour (Poisson arrivals), and it can serve 45 customers per hour (exponentially distributed). The salon is very crowded, so the manager wants to minimize the number of seats needed for waiting customers. At the same time, she doesnt want to lose too many customers who would leave when all waiting seats are occupied. Compute the fewest waiting seats that can be placed in the salon such that the probability of a customer balking and not entering the salon is less than 2.0%

Queuing Model with Unlimited Queue Size \begin{tabular}{|lr|} \hline Input (Arrival) Rate & 0.6 \\ \hline Service Rate & 0.8 \\ Activity (Service) Time T=1/ & 1.25 \\ \hline Number of Servers c & 1 \\ \hline \end{tabular} Note: c should be an integer \begin{tabular}{|lr|} \hline Average Queue Length Lq & 2.2500 \\ Average Number in the System L & 3.0000 \\ Average Wait for Jobs that Do Wait Wqw & 5.0000 \\ Average Wait in the Queue Wq & 3.7500 \\ Average Time in the System W & 5.0000 \\ Probability of an Empty System P0 & 25.00% \\ Probability of Waiting Pw & 75.00% \\ \hline \end{tabular} Queuing Computations developed by Chuck Munson, Washington State University. Varcinn 1. Nan 11 mnos Queuing Model with Limited Queue Size \begin{tabular}{|l|l|r|} \hline 2 & & \\ \hline 3 & Input (Arrival) Rate & 0.6 \\ 4 & Service Rate & 0.8 \\ 5 & Activity (Service) Time T=1/ & 1.25 \\ 6 & Number of Servers c & 2 \\ 7 & System Max K (Buffer =Kc ) & 99 \\ 8 & rho & 0.375 \\ \hline \end{tabular} 9 Notes: c and K should be integers; K must be c \begin{tabular}{lr|} \hline Average Queue Length Lq & 0.1227 \\ Average Number in the System L & 0.8727 \\ Average Wait for Jobs that Do Wait Wqw & 1.0000 \\ Average Wait in the Queue Wq & 0.2045 \\ Average Time in the System W & 1.4545 \\ Probability of an Empty System P0 & 45.45% \\ Probability of Blocking (Balking) Pb & 0.00% \\ Probability of Waiting (if not blocked) Pw & 20.45% \\ \hline \end{tabular} able of Results