Solve the problem for a Newtonian fluid with constsnt density and constant viscosity. Observe that the interface, the liquid's shear stress is zero since the viscosity of the gas is negligible compared to the liquid.

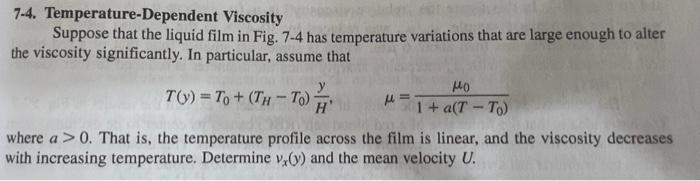
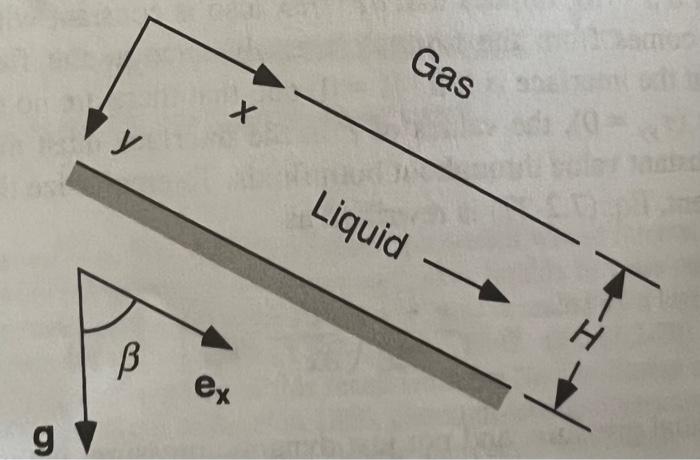
7-4. Temperature-Dependent Viscosity Suppose that the liquid film in Fig. 7-4 has temperature variations that are large enough to alter the viscosity significantly. In particular, assume that HO T(y) = To + (Tu - To 1 + a(T - TO M= where a > 0. That is, the temperature profile across the film is linear, and the viscosity decreases with increasing temperature. Determine vx(y) and the mean velocity U. Gas y Liquid lez I B. ex g