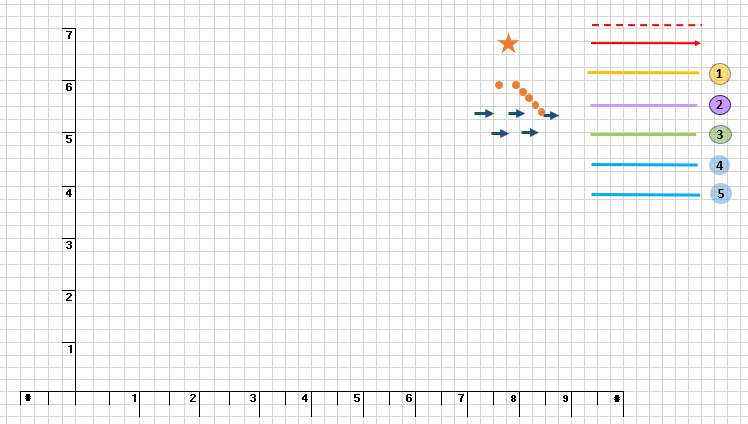
Solve the problem Graphically, Considering: 1. Feasibility Region: (15pts) - Draw the lines that represent each constraint to find the feasible region. You should show all the calculations to obtain full points. - Use a different color for each line and enumerate them. - If you find a feasible region, use a light color to differentiate it. 2. Gradient (3 pts) - Calculate the gradient of the objective function and draw it (using the given red arrow) 3. Level curves (3 pts) - Draw the objective function (using the given dashed red line) to do the search for the optimal solution. 4. Optimal solution (6 pts) - Indicate in the graph the optimal point using the given orange star. - Calculate the coordinates of the optimal point. You should show all the calculations to obtain full points. 5. Identify all feasible extreme points (also called corner points) (3 pts) - Identify feasible extreme points in the graph with the given orange dots NOTE: If you are working by hand, procure a neat handwriting and a quality pictures

Problem Minimize z= 6x1 + 8x2 Subject to: 4x1 + 3x2 > 15 1 4x2 > 8 2 x1 + x2 9 x1 > 0 4 x2 > 0 5 3 Extreme points: T - | | | - 7 | * 1 9 2 5 3 4 | 4 5 3 2 1 | C 2 5