solve the question using c programming (picture 2,3 and 4 are the manual calculation for question 6.55 stated)

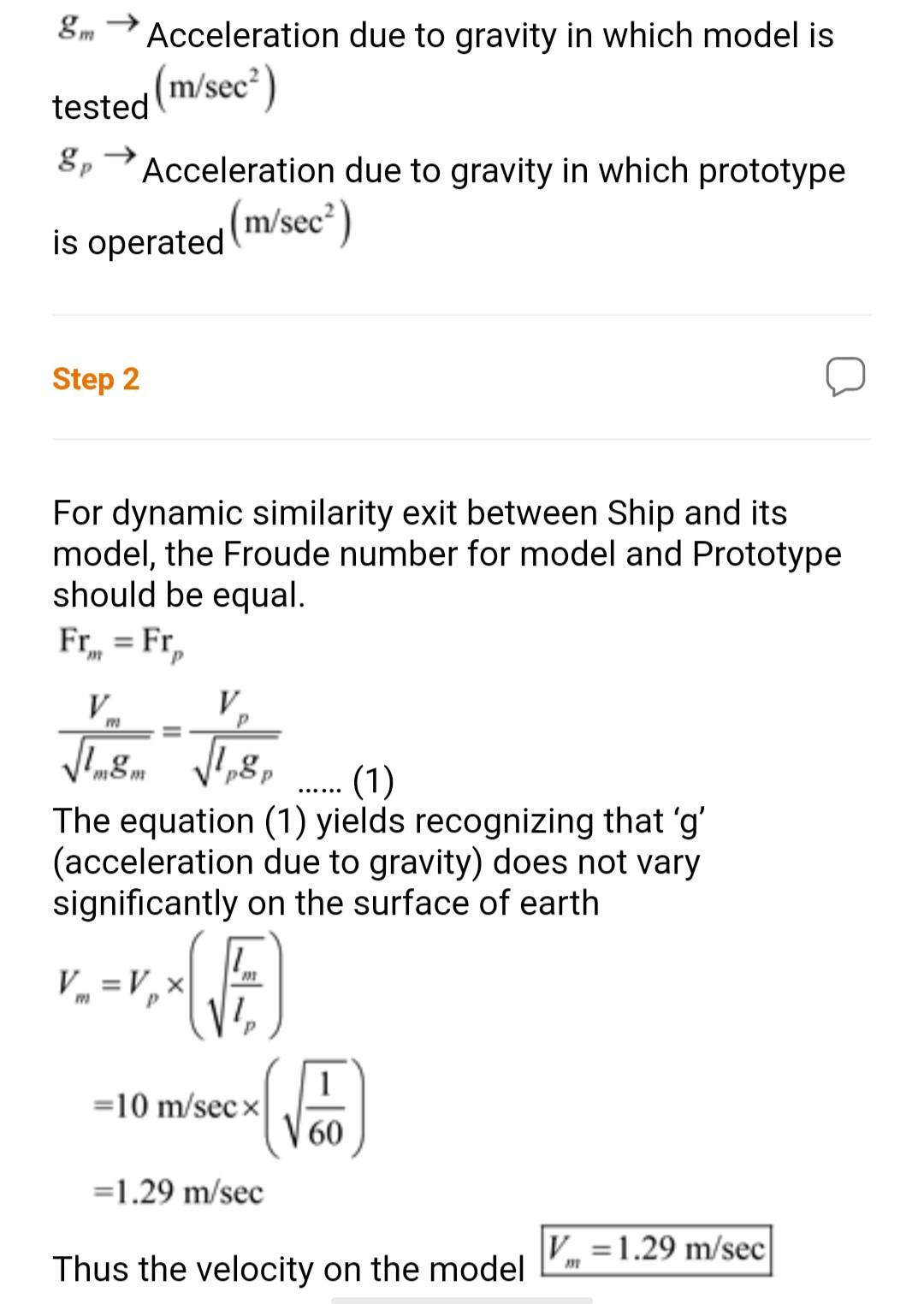
6.55 A 1:60 scale model of a ship is used in a water tank to simulate a ship speed of 10 m/s. What should be the model speed? If a towing force of 10 N is measured on the model, what force is expected on the prototype? Neglect viscous effects. Given: Prototype (Ship) and its model For Prototype Speed, V = 10 m/sec 0 Towing Force (F.), -2 Let's be Length of prototype (m) Let'm be Length of model (m) = 10 1. DIT Scale ratio of length, For model Speed ( m)? From = 10 N Towing Force, The variable used are Acceleration due to gravity in which model is 8m Acceleration due to gravity in which model is tested (m/sec) Acceleration due to gravity in which prototype is operated (m/sec) Step 2 For dynamic similarity exit between Ship and its model, the Froude number for model and Prototype should be equal. Fr, = Fr V Jg (1) The equation (1) yields recognizing that'g' (acceleration due to gravity) does not vary significantly on the surface of earth p van 1,8 01 V =V x 1 P =10 m/sec x 1 60 =1.29 m/sec V... = 1.29 m/sec Thus the velocity on the model The ratio of Towing force is found recognizing that Force (Fr) - mass x acceleration pt x 7 V X T LV plx=x- T 1 =PLV2 The ratio of forces of model to prototype is given by (Fr). P.D.V.? (F), P,DV? X 291 PP D (F1), = (Fr). D Since both the model and prototype are operated in same water facilities P = Pp 10 Fr, =10 Nx (1)x( 1.29 =10 NX 60X 3600 = 2160000 N = 2160 KN Thus the towing Force acting on the Prototype is (Fr), =2160 KN *(60)