Solve the word problem. Fill in the table as this will serve as your guide. Draw the curve, the rejection region, state the critical value and the computed value. Also do not forget to include the decision rule and the conclusion.

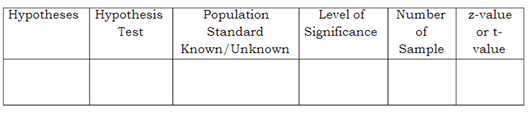
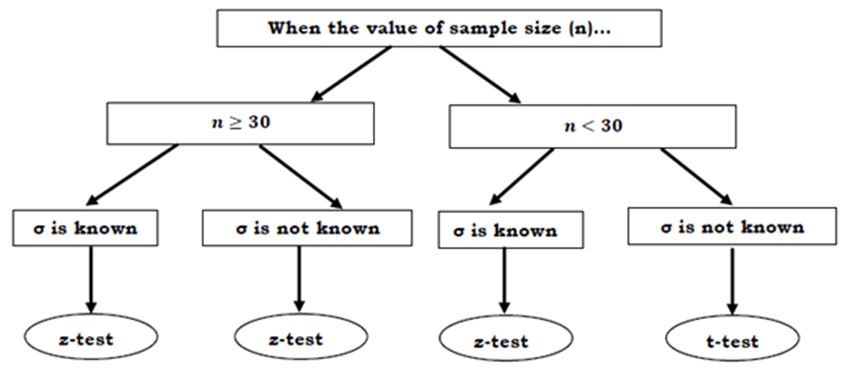
Hypotheses Hypothesis Population Level of Number z-value Test Standard Significance of or t- Known/Unknown Sample valueThe lCoronavirus Disease (COVID-lQ] is an infectious disease caused bv a new strain of coronavirus. The World Health Organization [WHO] claims that the incubation period of the virus in the infected person has a mean of 5.1 days. The doctors in the Philippines conducted a research and they found out that incubation period of the virus in human body:F is 5.03 days with a standard deviation of 3.32. The samples were 46 COVID patients. Is there enough evidence to conclude that the incubation period of the virus is 5.1 days as stated, at Cl=D.Ul? When the value of sample size (n)... n 2 30 n 70.95 b) Since h= 100 and n- 30, therefore we will 2- test. . According to the problem, the significance level () is 1%% or 0.01. This means that the confidence level (CL) is 99% or 0.99. Using a Z-Table, the critical value corresponding to a confidence level of 99% 2. 326 NOTES CRITICAL VALUE : Zcrit. = 2.326 zenit. = critical Z- value ( ) REJECTION REGION 0 Since we used an alternative hypothesis of HA: M > 70.95 , thus we will conduct right tailed test. . Also, the critical value is 2.326 2. 326 . As we can see , the rejection region is bounded from 2.326 up to o (infinity ) - 00 - + 0o Rejection region : Z = 2.326 Rejection region d ) TEST VALVE Formula : where 2 = 2 - value (test value ) 2 = X - M X = Sample mean : 73 (0/ Jn ) M = population mean : 70.95 Solution. 5 : population standard deviation : 8.1 2 = 73 - 70.95 n = sample size = 100 8 .1 Z = 2. 531 e) DECISION Rule 7: Reject Ho if Z 2 Ecrit (Accept HA) Rule 2: Do not reject Ho if E L Ecrit. ( Reject HA) . since Z = 2. 531 > Zcrit = 2. 326, thus we reject Ho, and accept HA. Decision: Reject the null hypothesis and conclude that the population mean is greater than 70.95