solve these practice problems

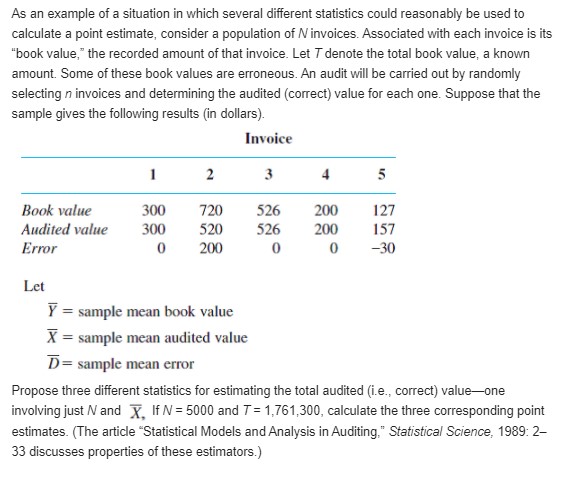
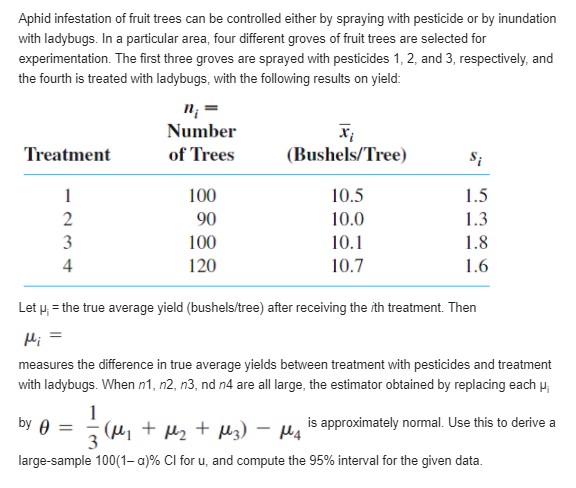
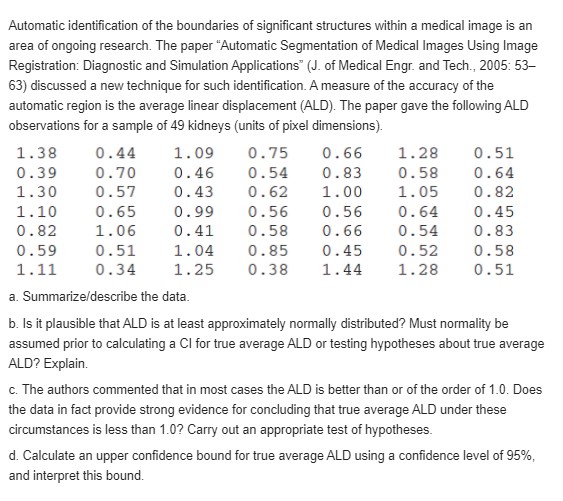
The difference between the number of customers in line at the express checkout and the number in line at the superexpress checkout in Exercise 3 is X, - X2 Calculate the expected difference. Reference Exercise 3 A certain market has both an express checkout line and a superexpress checkout line. Let X1 denote the number of customers in line at the express checkout at a particular time of day, and let X2 denote the number of customers in line at the superexpress checkout at the same time. Suppose the joint pmf of X1 and X2 is as given in the accompanying table. X a. What is P(X, = 1, X, = 1), that is, the probability that there is exactly one customer in each line? b. What is P(X, = X,), that is, the probability that the numbers of customers in the two lines are identical? c. Let A denote the event that there are at least two more customers in one line than in the other line. Express A in terms of X, and X2, and calculate the probability of this event. d. What is the probability that the total number of customers in the two lines is exactly four? At least four?The relative conductivity of a semiconductor device is determined by the amount of impurity "doped" into the device during its manufacture. A silicon diode to be used for a specific purpose requires an average cut-on voltage of .60 V, and if this is not achieved, the amount of impurity must be adjusted. A sample of diodes was selected and the cut-on voltage was determined. The accompanying SAS output resulted from a request to test the appropriate hypotheses. N Mean Std Dev T Prob. > T 15 0.0453333 0.0899100 1.9527887 0 . 0711 [Note: SAS explicitly tests Ho: u = 0, so to test H: u = .60, the null value .60 must be subtracted from each x ; the reported mean is then the average of the (x; - .60) values. Also, SAS's P-value is always for a two-tailed test.] What would be con- cluded for a significance level of .01? .05? .10? [Note: SAS explicitly tests Ho : p = 0, so to test Ho : p = .60, the null value .60 must be subtracted from each xi; the reported mean is then the average of the (x - .60)values. Also, SAS's P-value is always for a two-tailed test.] What would be concluded for a significance level of .01? .05? .10?Compute the correlation coefficient r for X and Y of Example 5.16 (the covariance has already been computed). Reference example 5.16 The joint and marginal pdf's of X = amount of almonds and Y = amount of cashews were D It might appear that the relationship in the insurance example is quite strong since Cov(X, Y ) = 1875, whereas Cov(X, n) = - in the nut example would seem to imply quite a weak relationship. Unfortunately, the covariance has a serious defect that makes it impossible to interpret a computed value. In the insurance example, suppose we had expressed the deductible amount in cents rather than in dollars. Then 100X would replace X, 100 Y would replace Y, and the resulting covariance would be Cov(100X, 100Y) = (100)(100)Cov(X, Y) = 18,750,000. If, on the other hand, the deductible amount had been expressed in hundreds of dollars, the computed covariance would have been (.01)(.01)(1875) = .1875. The defect of covariance is that its computed value depends critically on the units of measurement. Ideally, the choice of units should have no effect on a measure of strength of relationship. This is achieved by scaling the covariance.a. Let X, have a chi-squared distribution with parameter v1 (see Section 4.4), and let X, be independent of X, and have a chi-squared distribution with parameter v2- Use the technique of Example 5.21 to show that X, + X, has a chi-squared distribution with parameter V1 _ V2- b. In Exercise 71 of Chapter 4, you were asked to show that if Z is a standard normal rv, then Zz has a chi-squared distribution with v = 1. Let Z,, Z 2. .. .. Z, ben independent standard normal ry's. What is the distribution of X? Justify your answer. c. Let X1, . . . . X, be a random sample from a normal distribution with mean m and variance of. What is the distribution of the sum 1 ? Justify your answer. Reference example 5.21 Service time for a certain type of bank transaction is a random variable having an exponential distribution with parameter I. Suppose X1 and X2 are service times for two different customers, assumed independent of each other. Consider the total service time To = X1 + X2 for the two customers, also a statistic. The cdf of 7, is, for f 2 0, X2 Reference exercise 7 in chapter 4 The time X (min) for a lab assistant to prepare the equipment for a certain experiment is believed to have a uniform distribution with A = 25 and B =35. a. Determine the pdf of X and sketch the corresponding density curve. b. What is the probability that preparation time exceeds 33 min? c. What is the probability that preparation time is within 2 min of the mean time? [Hint. Identify u from the graph of f(x).] d. For any a such that 25