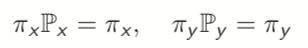
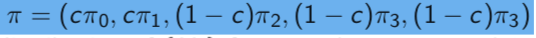
Stationary Distribution May Not Be Unique Consider a Markov chain with transition matrix I of the form O 4 O O U - PX O \\A N M + PY , O This Markov chain has 2 classes (0 , 1 ] and [2 , 3 , 4] , both closed and recurrent . So this Markov chain can be reduced to two sub - Markov chains , one with state space (0 . 1 ] and the other (2 , 3 , 4 } . Their transition matrices are respectively PX and Py* Say TIX = ( TTO , IT1 ) and Tly = ( TT2 , 13 , ITA ) be respectively the stationary distributions of the two sub-Markov chains , i.e .. IT * PX = TX , TyLy = TTY Verify that IT = ( CITO , CITI , ( 1 - C ) ITZ , ( 1 - C ) IT3, ( 1 - C ) IT3 ) is a stationary distribution of{ X~ } for any c between O and 1 . Lecture 4 ~ }\f\f