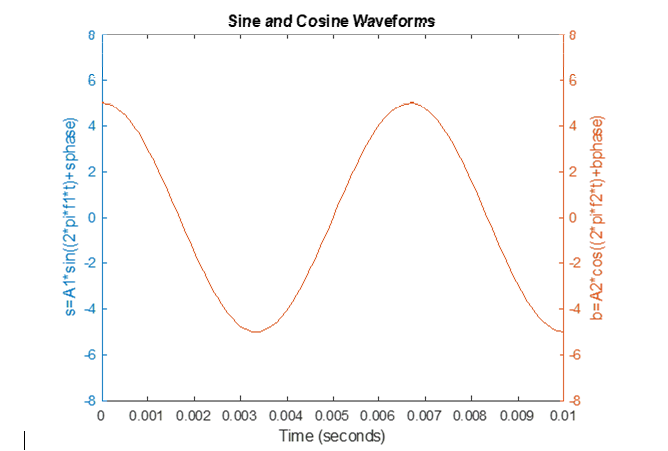
Step 1.9 Using the MatLab code in step 1.8, modify the following: (1) s(t) = s=A1*sin((2*pi*f1*t)+sphase) = 5sin(2150t + /2) (2)

b(t) = b=A2*cos((2*pi*f2*t)+bphase) = 5cos(2150t + 0)

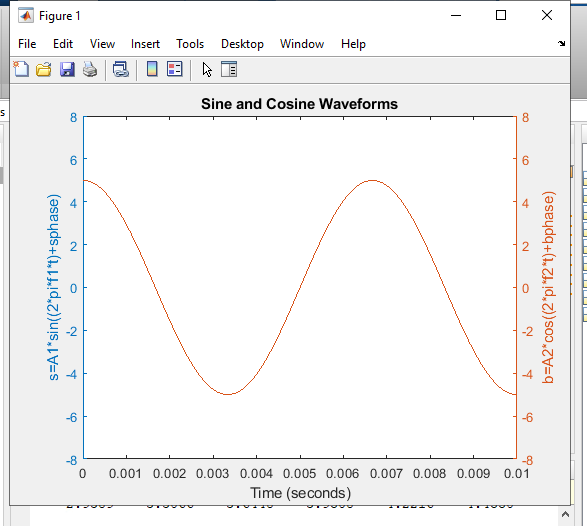
Question 1. Select the best answer regarding your observation from step 1.9.

a. both s and b appear as identical sine waves

b. both s and b appear as identical cosine waves

c. both s and b appear as cosine waves; however, their amplitudes differ

d. s appears as a sine wave while b appears as a cosine wave; both have different amplitudes.

Using MatLab can anyone help me with this question? (the second graph is after the changes being made)

Sine and Cosine Waveforms S=A1* sin((2pi*f1*t)+sphase) b=A2*cos((2* pi* f2*t) +bphase) 0 0.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008 0.009 Time (seconds) 0.01 - O X Figure 1 File Edit O View Help Insert Tools O E Desktop Window E Sine and Cosine Waveforms s=A1* sin((2pif1*t)+sphase) b=A2*cos((2pif2t)+bphase) 0 0.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008 0.009 0.01 Time (seconds)