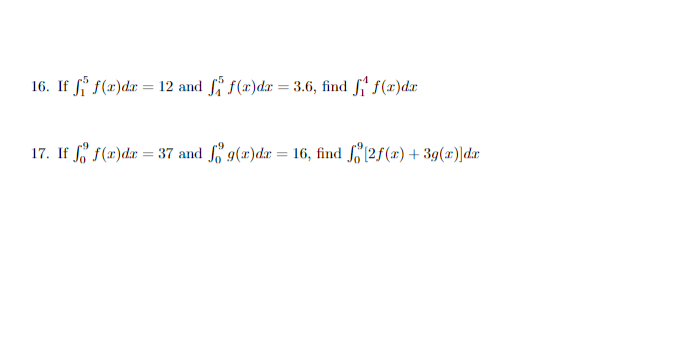
Study Guide for Exam 2 Math 150A 1. Verify that the function satisfies the three hypotheses of Rolle's Theorem on the given interval. Then find all numvers c that satisfy the conclusion of Rolle's Theorem. (a) f(x) = x2 + 4x +5; [-3, -1] (b) f(x) = 23 -4x2 -2+7; [-1, 4) (c) f(x) = sin(2:), [-7, "] 2. Verify that the function satisfies the hypotheses of the Mean Value The- orem on the given interval. Then find all the numbers c that satisfy the conclusion of the Mean Value Theorem. (a) f(x) = -23 +4x2 -3; [0, 4) (b) f(x) = 42; (c) f(x) = 1248: [-3, -1) 3. Suppose that f(0) = 2 and f'(x) 2 4 for all values of 2. How small can f(3) possibly be? 4. Suppose that f(1) = 5 and f'(x) 0 on (-06, 0)U(2, 4), f'(x) 0 on (1,3), f"(x) 0, f(1) =6 (c) f"(x) = -2+12x - 12x2, f(0) = 4, f'(0) = 12 (d) f"(x) = sina + cost, f(0) = 3, f'(0) = 4 (e) f"(x) = 2et + 3sina, f(0) = 0, f(#) =0 15. A particle is moving with the given data. Find the position of the particle. (a) v(t) = sint - cost, s(0) = 0 (b) a(t) = 10sint + 3cost, s(0) = 0, s(2n) = 1216. If fi f(x)dr = 12 and [i f(x)dx = 3.6, find fif(x)de 17. If fo f(x)de = 37 and Jo g(x)de = 16, find Jo [2f(x) + 3g(x)]dx