SUBJECT: COMPUTATION THEORY (TRUE or FALSE)

Please answer true or false for all questions below:

1. For the alphabet, 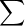= {a, b},

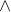is a string in *

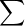2. For the alphabet, 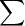= {a, b},

if x represents a character from 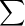, then xbx could represent the string, abb

3. For the alphabet, 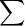= {a, b},

if S = {aa, b}, then bbaaa 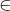S*

4. For the alphabet, 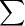= {a, b},

the string, bb, can be generated from the regular expression, b a* b*

5. For the alphabet, 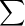= {a, b},

The string, baab, can be generated from the regular expression, b* (ab)*

6. For the alphabet, 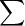= {a, b},

the string, 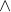, is in the language, L ( (a a* + b)* )

7. For the alphabet, 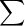= {a, b},

the string, abba, is in the language, L (a (a + bb)* )

8. For the alphabet, 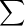= {a, b},

the two regular expressions, a*b (a+b)8 and (a + b)* b a* represent the same language.