Submit a plain text file indicating where the languages listed below should be placed on the onion diagram.

Onion Diagram:

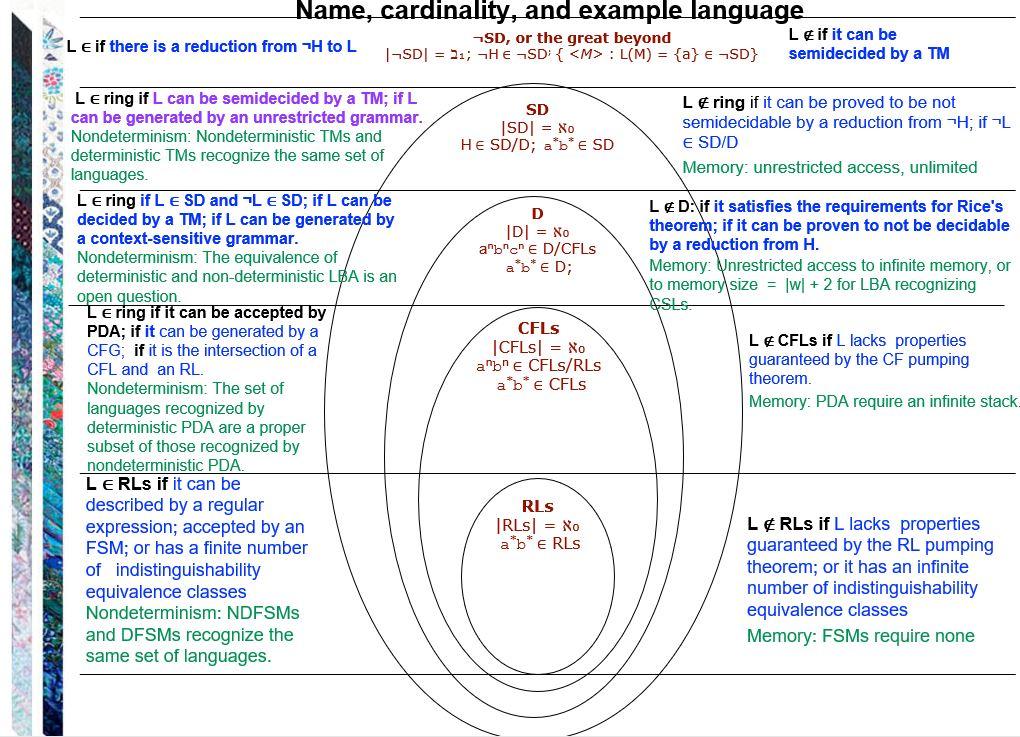
L16 = { w: w is a grammatical sentence in the Swiss dialect of the German language} { = {0,1}, L17 = { : 0 L(M) } L18 = { : L(M1) = L(M2) } L19 = {

: P is syntactically correct Python source code.} L20 = {

: where P is syntactically correct Python source code, and w is an arbitrary string in E*. When P is executed by a Python interpreter, it will halt on input w} Name, cardinality, and example language Le if there is a reduction from PH to L -SD, or the great beyond Leif it can be [SDT = 21; { : L(M) = {a} + HSD} semidecided by a TM SD |SD| = No HE SD/D; a'b* E SD Le ring if it can be proved to be not semidecidable by a reduction from "H; if L E SD/D Memory: unrestricted access, unlimited D 1D = No a"b"c" e D/CFLs a'b* eD; L&D. if it satisfies the requirements for Rice's theorem; if it can be proven to not be decidable by a reduction from H. Memory: Unrestricted access to infinite memory, or to memory size = [w] + 2 for LBA recognizing SLS Lering if L can be semidecided by a TM; if L can be generated by an unrestricted grammar. Nondeterminism: Nondeterministic TMs and deterministic TMs recognize the same set of languages Le ring if Le SD and Le SD; if L can be decided by a TM; if L can be generated by a context-sensitive grammar. Nondeterminism: The equivalence of deterministic and non-deterministic LBA is an open question. Le ring if it can be accepted by PDA; if it can be generated by a CFG; if it is the intersection of a CFL and an RL. Nondeterminism: The set of languages recognized by deterministic PDA are a proper subset of those recognized by nondeterministic PDA. LERLs if it can be described by a regular expression; accepted by an FSM; or has a finite number of indistinguishability equivalence classes Nondeterminism: NDFSMS and DFSMs recognize the same set of languages. CFLS CFLs = Xo a"b" e CFLS/RLS a*b* e CFLs L&CFLs if L lacks properties guaranteed by the CF pumping theorem. Memory: PDA require an infinite stack. RLS IRLS = Xo a b E RLS L&RLs if L lacks properties guaranteed by the RL pumping theorem; or it has an infinite number of indistinguishability equivalence classes Memory: FSMs require none L16 = { w: w is a grammatical sentence in the Swiss dialect of the German language} { = {0,1}, L17 = { : 0 L(M) } L18 = { : L(M1) = L(M2) } L19 = {

: P is syntactically correct Python source code.} L20 = {

: where P is syntactically correct Python source code, and w is an arbitrary string in E*. When P is executed by a Python interpreter, it will halt on input w} Name, cardinality, and example language Le if there is a reduction from PH to L -SD, or the great beyond Leif it can be [SDT = 21; { : L(M) = {a} + HSD} semidecided by a TM SD |SD| = No HE SD/D; a'b* E SD Le ring if it can be proved to be not semidecidable by a reduction from "H; if L E SD/D Memory: unrestricted access, unlimited D 1D = No a"b"c" e D/CFLs a'b* eD; L&D. if it satisfies the requirements for Rice's theorem; if it can be proven to not be decidable by a reduction from H. Memory: Unrestricted access to infinite memory, or to memory size = [w] + 2 for LBA recognizing SLS Lering if L can be semidecided by a TM; if L can be generated by an unrestricted grammar. Nondeterminism: Nondeterministic TMs and deterministic TMs recognize the same set of languages Le ring if Le SD and Le SD; if L can be decided by a TM; if L can be generated by a context-sensitive grammar. Nondeterminism: The equivalence of deterministic and non-deterministic LBA is an open question. Le ring if it can be accepted by PDA; if it can be generated by a CFG; if it is the intersection of a CFL and an RL. Nondeterminism: The set of languages recognized by deterministic PDA are a proper subset of those recognized by nondeterministic PDA. LERLs if it can be described by a regular expression; accepted by an FSM; or has a finite number of indistinguishability equivalence classes Nondeterminism: NDFSMS and DFSMs recognize the same set of languages. CFLS CFLs = Xo a"b" e CFLS/RLS a*b* e CFLs L&CFLs if L lacks properties guaranteed by the CF pumping theorem. Memory: PDA require an infinite stack. RLS IRLS = Xo a b E RLS L&RLs if L lacks properties guaranteed by the RL pumping theorem; or it has an infinite number of indistinguishability equivalence classes Memory: FSMs require none