Question: Suppose a 3 x 3 real matrix A has only two (real) distinct eigenvalues. Suppose that tr(A) = -4 and det(A) = smaller eigenvalue

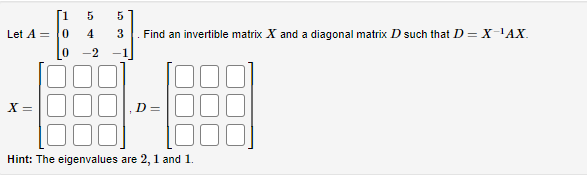
Suppose a 3 x 3 real matrix A has only two (real) distinct eigenvalues. Suppose that tr(A) = -4 and det(A) = smaller eigenvalue = larger eigenvalue = has multiplicity | has mulitiplicity and -32. Find the eigenvalues of A with their algebraic multiplicities. 11 21 Let M = Find formulas for the entries of M", where n is a positive integer. MT= [1 5 5 Let A = 0 4 3 0 -2 x = Find an invertible matrix X and a diagonal matrix D such that D = X-AX. D = Hint: The eigenvalues are 2, 1 and 1.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Required Use the following information to prepare a multistep income statement and a classified balance sheet for Eller Equipment Company for Year 2. (Hint: Some of the items will not appear on...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

CANMNMM January of this year. (a) Each item will be held in a record. Describe all the data structures that must refer to these records to implement the required functionality. Describe all the...

Suppose a 3 x 3 real matrix A has only two (real) distinct eigenvalues. Suppose that tr(A) = -4 and det(A) = -32. Find the eigenvalues of A with their algebraic multiplicities. smaller eigenvalue =...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

breif answers will be fine thanks ! (1 point) 3 -2 -2 The matrix A = 2 1 0 0 2 5 has one real eigenvalue. Find this eigenvalue, its multiplicity, and the dimension of the corresponding eigenspace....

1. Let A and B be 3 X 3 real matrices that commute: AB 2 BA. If .35, is a real eigenvalue of A. let V}. be the real subspace of ail eigenvectors having this eigenvalue. {a} Show that if V). is...

Eigenvalue/Eigenvector Part IV: Suppose A is an n x n matrix. a. What does it mean to say that a vector x E Rn is an eigenvector of A? b. Suppose A E R is an eigenvalue of A. What is the eigenspace...

Can you please help me with number 21. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! Open with Chapter 5 Linear Systems...

Can you please help me with number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! Linear Systems quations 406 The...

The BigRig Trucking Company participates in an Internet transportation exchange where customers advertise their shipments including load weight and volume, and trip origin and destination. BigRig...

A bank has currently the following balance sheet structure: (4 marks) Assets ($ million) Liabilities ($ million) Cash 100 Customer deposits 700 Debt securities issued by the government of Japan 50...

1 try left results when consumers believe that various brands provide the same set of attributes. Brand identification Brand parity Generic branding Brand loyalty

The following financial information (in US$ millions) is for two major corporations for the three years ended December 31: Instructions (a) Calculate the inventory turnover, days sales in inventory,...

(a) Find the generating function for the number of ways to select 10 candy bars from large supplies of six different kinds. (b) Find the generating function for the number of ways to select, with...

Rieger International is attempting to evaluate the feasibility of investing $95,000 in a piece of equipment that has a 5-year life. The firm has estimated the cash inflows associated with the...

"This system of n linear equations with n unknowns," said the Great Mathematician, "has a curious property." "Good heavens!" said the Poor Nut, "What is it?" "Note," said the Great Mathematician,...

(a)Prove that an orthogonal 2 ( 2 matrix must have the form Where Is a unit vector. (b)Using part (a), show that every orthogonal 2 ( 2 matrix is of the form Where 0 ( ( ( 2 (. or cos sin -sin cos...

6 Theory of Machines 5. A shaft carries five masses A, B, C, D and E which revolve at the same radius in planes which are equidistant from one another. The magnitude of the masses in planes A, C and...

In a one-dimensional boundary value problem with a no-flux condition on the left boundary, what is the relationship between the fictitious node and the nodes in the domain?

Use RK4 to find the solution to subject to the initial conditions y(0) = 1, y(0) = 1/2, y(0) = 1/3, y= 1/4, and y = 1/5. Your program should make a plot of the fourth derivative of y versus the...

What is the output of the following MATLAB code? 1 2 3 4 5 6 7 counter = 3; 8 stop = 0; 9 10 11 12 N 13 function out = 15 16 17 for i = 4:-1:1 x(i) = 1^2; end while stop == 0; end problem1_36 if x...

With many alternatives, why do you think that we have continued to rely so much on oil and other hydrocarbons?

What is an oligopoly?

Although energy is barely discussed in physiocratic, classical, or neoclassical economics, explain how each of these schools of economic thought focuses on the dominant energy flows of their time.