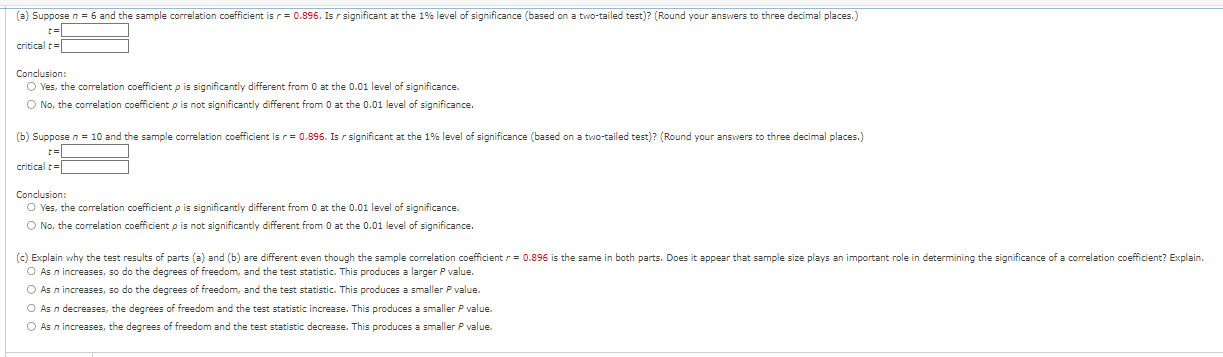
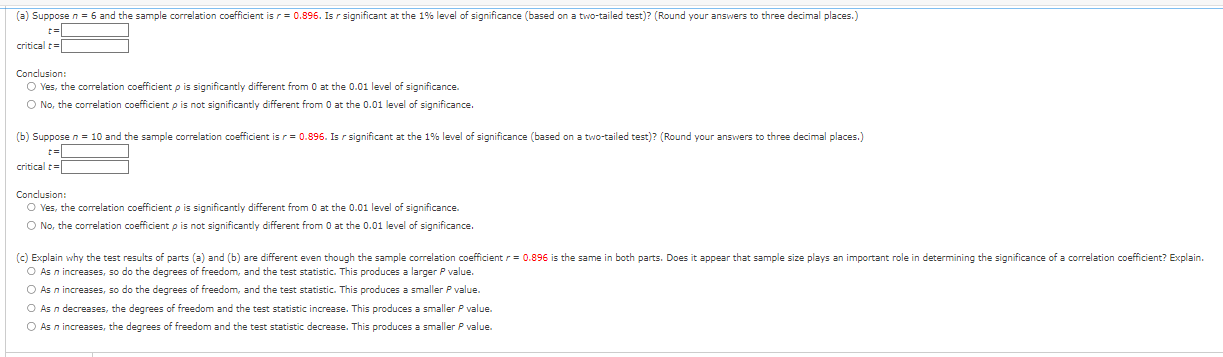
(@) Suppose n = 6 and the sample correlation coefficient is r = 0.896. Is / significant at the 1% level of significance (based on a two-tailed test)? (Round your answers to three decimal places.) 1= critical t= Conclusion: O Yes, the correlation coefficient p is significantly different from 0 at the 0.01 level of significance. O No, the correlation coefficient p is not significantly different from 0 at the 0.01 level of significance. (b) Suppose n = 10 and the sample correlation coefficient is r = 0.896. Is / significant at the 1%% level of significance (based on a two-tailed test)? (Round your answers to three decimal places.) t= critical t = Conclusion: O Yes, the correlation coefficient p is significantly different from 0 at the 0.01 level of significance. O No, the correlation coefficient p is not significantly different from 0 at the 0.01 level of significance. (c) Explain why the test results of parts (e) and (b) are different even though the sample correlation coefficient / = 0.896 is the same in both parts. Does it appear that sample size plays an important role in determining the significance of a correlation coefficient? Explain. O As n increases, so do the degrees of freedom, and the test statistic. This produces a larger P value. O As n increases, so do the degrees of freedom, and the test statistic. This produces a smaller P value. O As n decreases, the degrees of freedom and the test statistic increase. This produces a smaller P value. O As n increases, the degrees of freedom and the test statistic decrease. This produces a smaller P value