Suppose we are training a logistic classifier to solve a binary classification problem (i.e. we are performing logistic regression). The classifier corresponds to a function of the formh(x) =1/1+e?w^T x whose output is an estimate of the probability thatxbelongs to class 1.

Suppose while performing gradient ascent, the weights becomewT= [3,?5,?6].

The table below shows the result of using these weights to predict the class on the training examples

x1 x2 h(x) y

1 0.49 0.09 0.502 0

2 1.69 0.04 0.003 0

3 0.04 0.64 0.261 0

4 1. 0.16 0.049 0

5 0.16 0.09 0.840 1

6 0.25 0. 0.852 1

7 0.49 0. 0.634 1

8 0.04 0.01 0.939 1

(a)For a decision boundary of 0.5, create the confusion matrix.

(b)Plot the points on a graph and draw the decision boundary (I would suggest using some sort of plotting library and a image editor)

(c)For the data set above what is the FPR?

(d)For the data set above what is the TPR?

(e)What is the accuracy?

(f)What is the recall?

(g)What is the precision?

(h)In logistic regression, we are trying to maximize the log likelihood

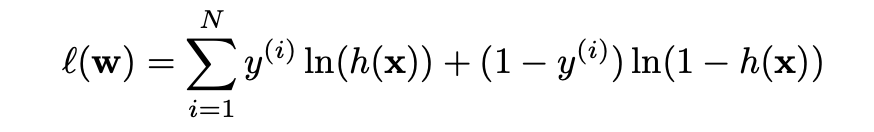
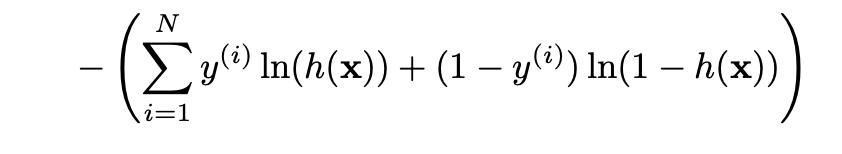
\f\f