Suppose we have a function f : R² R:

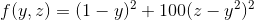
(1) Compute the gradient, 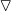f(x), where x = (y,z)^T .

(2) Compute the Hessian matrix, H(x).

(3) Find the minimum of the above function. To this end, with f(x) and H(x) in (1) and (2), write your R code to implement the Newton-Raphson algorithm. Test your code with the initial values x0 = c(2,2) and x0 = c(0,3), respectively.

(4) Make an R code to find the minimum using the steepest descent algorithm equipped with backtracking procedure.

The steepest descent algorithm:

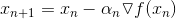
where 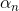> 0. The backtracking procedure is as follows:

(i) Start with 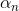= 1. (ii) Compute x_n+1 with .

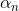(iii) If f(x_n+1) n), then increment n. Otherwise, set 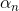= 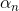/2, and go back to Step (ii).

Transcribed image text