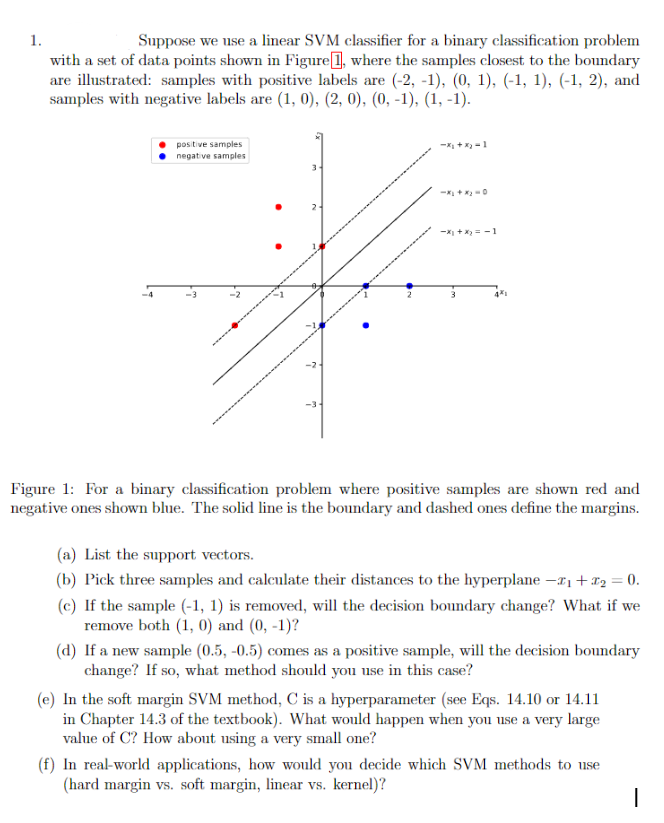
Suppose we use a linear SVM classifier for a binary classification problem

with a set of data points shown in Figure$[1,$ where the samples closest to the boundary

are illustrated: samples with positive labels are $(-2,-1),(0,1),(-1,1),(-1,2),$ and

samples with negative labels are $(1,0),(2,0),(0,-1),(1,-1).$

Figure $1$: For a binary classification problem where positive samples are shown red and

negative ones shown blue. The solid line is the boundary and dashed ones define the margins.

$($a$)$ List the support vectors.

$($b$)$ Pick three samples and calculate their distances to the hyperplane $-x_1+x_2=0.$

$($c$)$ If the sample $(-1,1)$ is removed, will the decision boundary change? What if we

remove both $(1,0)$ and $(0,-1)?$

$($d$)$ If a new sample $(0\mathrm{.}5,-0\mathrm{.}5)$ comes as a positive sample, will the decision boundary

change? If so$,$ what method should you use in this case?

$($e$)$ In the soft margin SVM method, C is a hyperparameter $($see Eqs. $14\mathrm{.}10$ or $14\mathrm{.}11$

in Chapter $14\mathrm{.}3$ of the textbook$).$ What would happen when you use a very large

value of $C?$ How about using a very small one?

$($f$)$ In real$-$world applications, how would you decide which SVM methods to use

$($hard margin vs$.$ soft margin, linear vs$.$ kernel$)?$