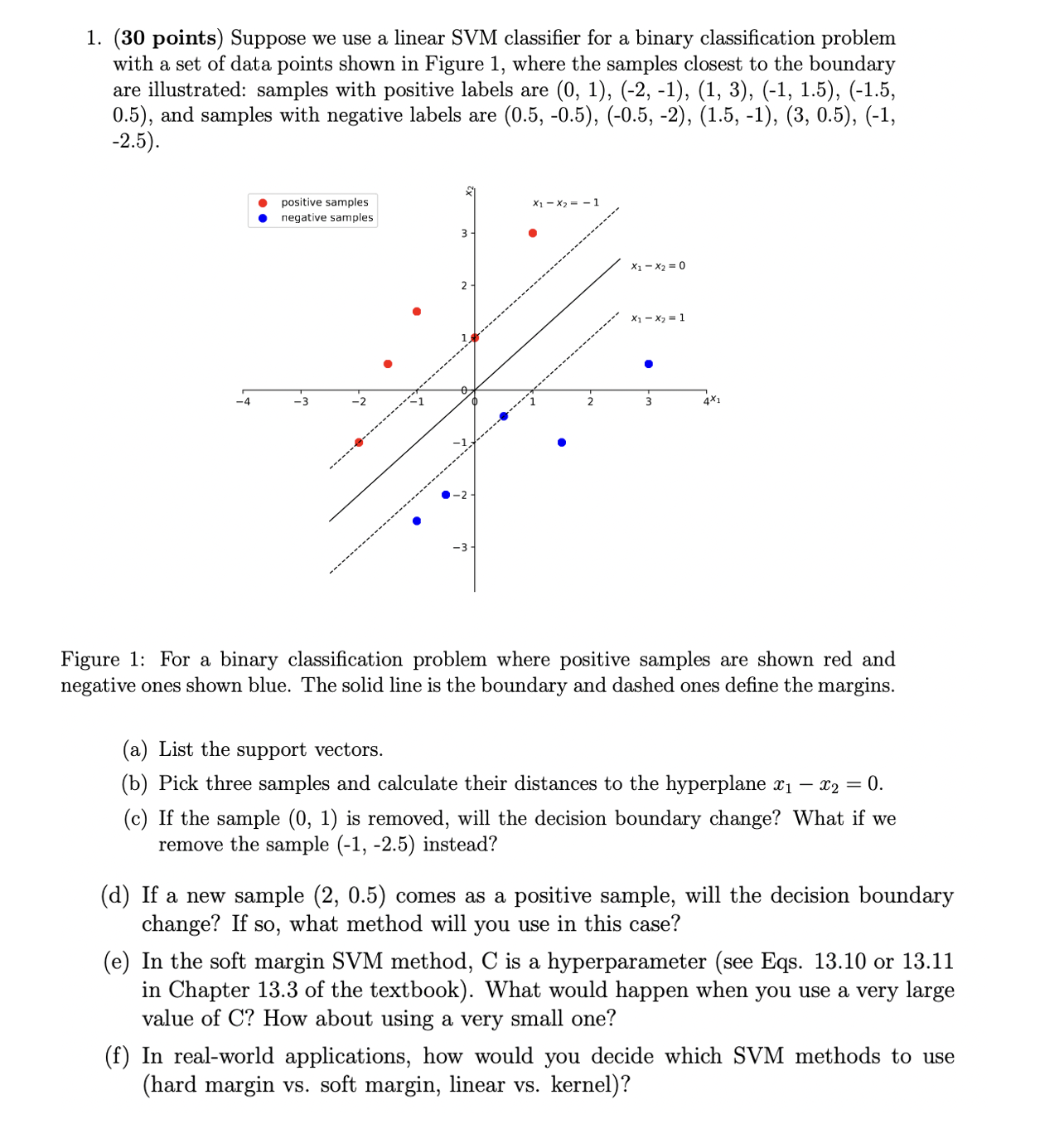
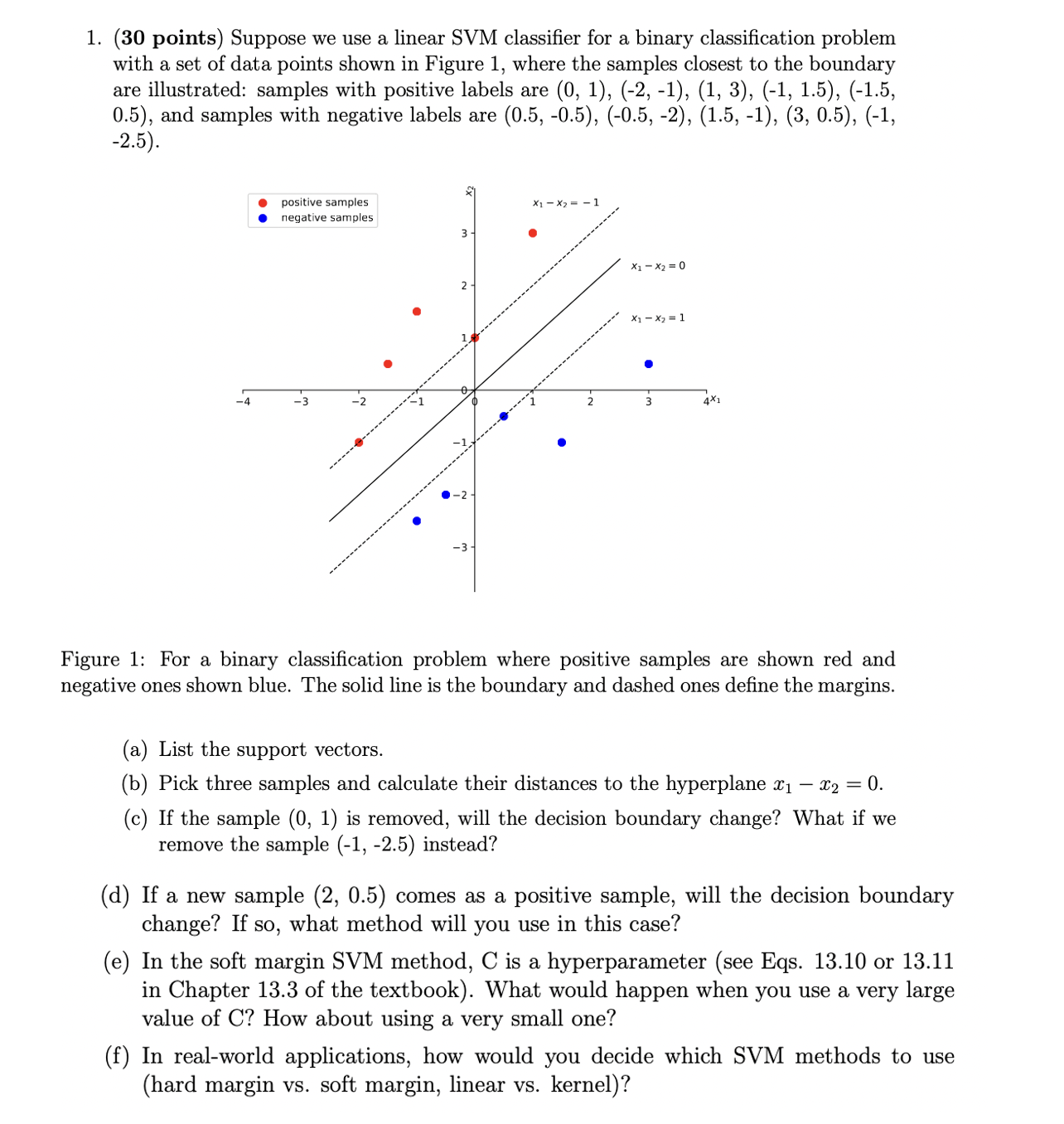
1. (30 points) Suppose we use a linear SVM classifier for a binary classification problem with a set of data points shown in Figure 1, where the samples closest to the boundary are illustrated: samples with positive labels are (0, 1), (-2, -1), (1, 3), (-1, 1.5), (-1.5, 0.5), and samples with negative labels are (0.5, -0.5), (-0.5, -2), (1.5, -1), (3, 0.5), (-1, -2.5) . positive samples X1 - X2 = - . . negative samples 2 (1 - X2 = 0 *1 - X2 = 1 4 - 3 -2 -1 2 3 4X -3 Figure 1: For a binary classification problem where positive samples are shown red and negative ones shown blue. The solid line is the boundary and dashed ones define the margins. (a) List the support vectors. (b) Pick three samples and calculate their distances to the hyperplane X1 - X2 = 0. (c) If the sample (0, 1) is removed, will the decision boundary change? What if we remove the sample (-1, -2.5) instead? d) If a new sample (2, 0.5) comes as a positive sample, will the decision boundary change? If so, what method will you use in this case? (e) In the soft margin SVM method, C is a hyperparameter (see Eqs. 13.10 or 13.11 in Chapter 13.3 of the textbook). What would happen when you use a very large value of C? How about using a very small one? (f) In real-world applications, how would you decide which SVM methods to use (hard margin vs. soft margin, linear vs. kernel)