The answer is

the important part is 1b and 1c thank you

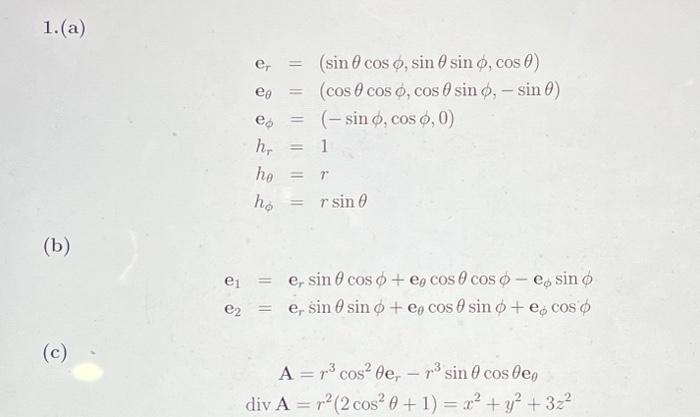
Spherical polar coordinates (r,,) are defined by the transformation equations x=rsincos,y=rsinsin,z=rcos (a) From the above transformation equations (not from memory!), find the unit vectors er,e,e of spherical polar coordinates and their associated scale factors hr,h and h. (b) Hence show that the Cartesian basis vector in the z direction, e3, can be written as e3=cosersine and also express e1 and e2 in the spherical polar basis. (Hint: You might find it useful first to construct the vector siner+cose.) (c) The vector field A has Cartesian components (0,0,x2z+y2z+z3). Express A entirely in the spherical polar basis (i.e. using spherical polar coordinates and basis vectors). Hence, evaluate its divergence using the formula F=r21r(r2Fr)+rsin1[(sinF)+F] for a vector field F with spherical polar components Fr,F0 and F. Check your answer by evaluating div A in Cartesian coordinates. 1.(a) er=(sincos,sinsin,cos)e=(coscos,cossin,sin)e=(sin,cos,0)hr=1h=rh=rsin (b) e1=ersincos+ecoscosesine2=ersinsin+ecossin+ecos (c) A=r3cos2err3sincosedivA=r2(2cos2+1)=x2+y2+3z2