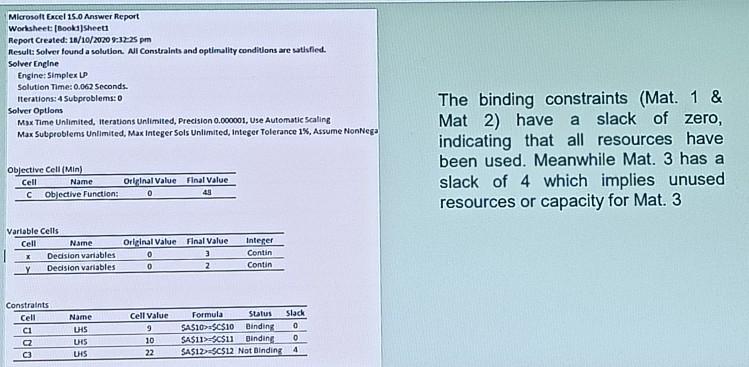
The binding constraints (mat. 1& mat 2) have a stack of zero, indicating that all resources have been used. Meanwhile mat 3 has a slack of 4 which implies unused resources or capacity for mat 3

Based on the computer solution what happens to the optimal solution if the RHS of material 2 will be changed to 14? Interpret the result.

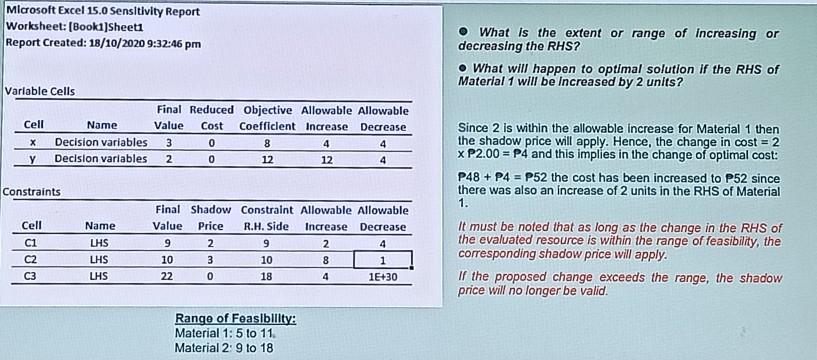
Let x-quantity of product A A B D y-quantity of product B Objective Function: 48 Minimize C = P8x + P12y Decision variables 3 2 Subject to: Y Constraints x + 3y29 Material 1 LHS Inequality Symbol RHS 2x + 2y 2 10 Material 2 9 9 6x + 2y 18 Material 3 10 IV IV IV 10 22 18 x, y20 Microsoft Excel 15.0 Answer Report Worksheet (Booksheet Report Created: 10/10/2020 7:32:25 pm Result: Solver found a solution. All Constraints and optimality conditions are satisfied. Solver Engine Engine: Simplex LP Solution Time: 0.062 Seconds. Iterations: 4 Subproblems: 0 Solver Options Max Time Unlimited. Iterations Unlimited, Precision 0.000001, Use Automatic Scaling Max Subproblems Unlimited, Max Integer Sols Unlimited, Integer Tolerance 1%. Assume NonNega The binding constraints (Mat. 1 & Mat 2) have a slack of zero, indicating that all resources have been used. Meanwhile Mat. 3 has a slack of 4 which implies unused resources or capacity for Mat. 3 Objective Cell (Min) Cell Name cObjective Function: Orlyinal Value Final Value 48 Variable Cells Cell Name Decision variables Y Decision variables Orleinal Value Final Value 0 0 2 Interer Contin Contin Constraints Cell C1 Status Name UHS U15 US Cell Value 9 10 22 Formula Slack SAS10>$C$10 binding 0 SA$11>$C$11 binding 0 SAS12SCS12 Not Dinding C3 Microsoft Excel 15.0 Sensitivity Report Worksheet: (Booki]Sheet1 Report Created: 18/10/2020 9:32:46 pm What is the extent or range of increasing or decreasing the RHS? . What will happen to optimal solution if the RHS of Material 1 will be increased by 2 units? Variable Cells Cell X Name Decision variables Decision variables Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 3 0 8 4 4 2 0 12 12 4 Y Constraints Since 2 is within the allowable increase for Material 1 then the shadow price will apply. Hence, the change in cost = 2 XP2.00 = P4 and this implies in the change of optimal cost: P48 + P4 = P52 the cost has been increased to P52 since there was also an increase of 2 units in the RHS of Material 1. It must be noted that as long as the change in the RHS of the evaluated resource is within the range of feasibility, the corresponding shadow price will apply. If the proposed change exceeds the range, the shadow price will no longer be valid. Cell C1 C2 C3 Final Shadow Constraint Allowable Allowable Value Price R.H. Side Increase Decrease 9 2 9 2 4 10 3 10 8 1 22 0 18 4 1E+30 Name LHS LHS LHS Range of Feasibility: Material 1: 5 to 11. Material 2:9 to 18