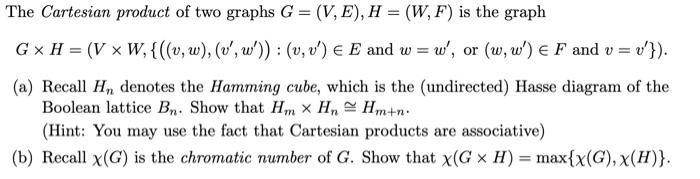
The Cartesian product of two graphs G = (V, E), H = (W, F) is the graph GxH = (V x W, {((v, w), (v', w')) : (v, v') e E and w = w', or (w, w') E F and v = v'}). (a) Recall H, denotes the Hamming cube, which is the (undirected) Hasse diagram of the Boolean lattice Bn. Show that Hm x Hn Hm+n. (Hint: You may use the fact that Cartesian products are associative) (b) Recall x(G) is the chromatic number of G. Show that x(G x H) = max{x(G), X(H)}.