Question: The colored writing below are the notes my professor is asking the work to be done like. I'm unsure as he didn't like the way



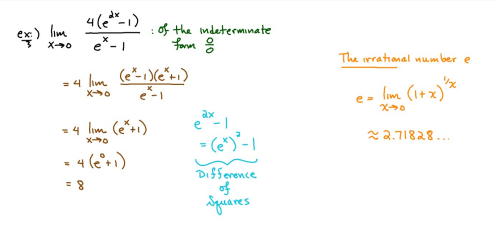


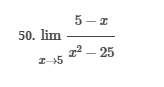
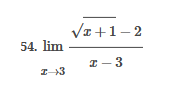
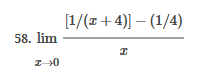
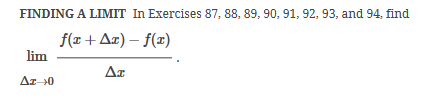
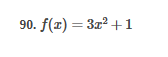

![3 ) (x-2 ) ( x-2)[x3 - 9x ] 3 (-4)-1 4(x+3](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666501063c53b_430666501062a1ae.jpg)

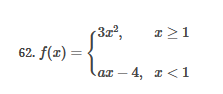
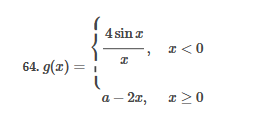


![the interval [ a, 6] has at least one zero on the](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66650107c4b3c_43166650107b0a03.jpg)
![iis fras # f(b) interval [o, or] and k is any value](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6665010808ad9_43166650107eb0a6.jpg)
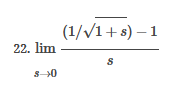
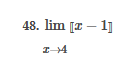
The colored writing below are the notes my professor is asking the work to be done like. I'm unsure as he didn't like the way my work is done.



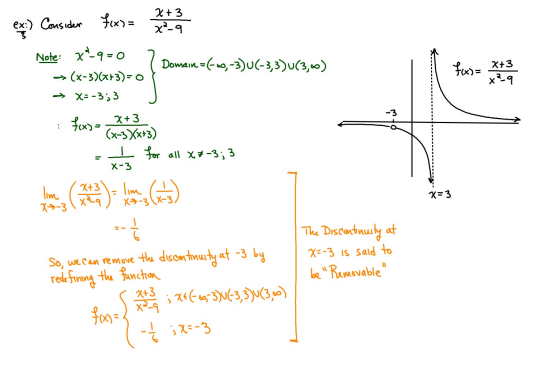
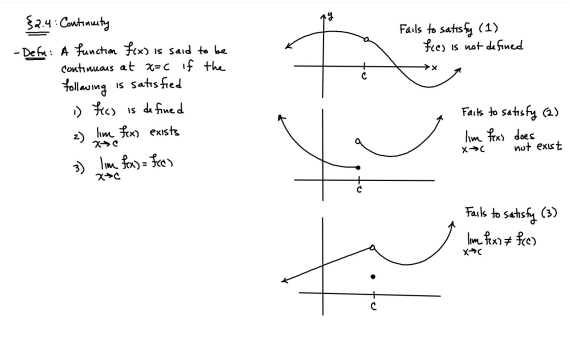
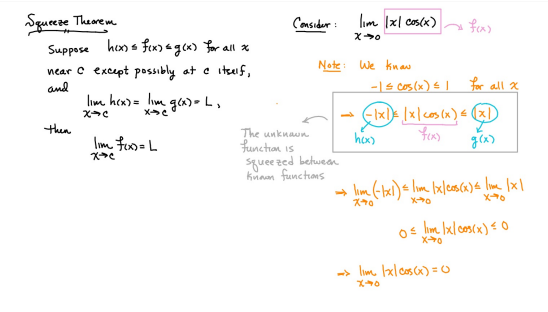
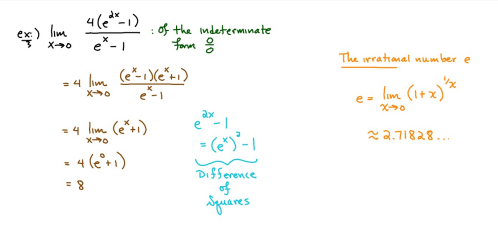


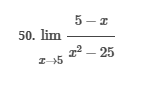
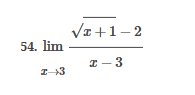
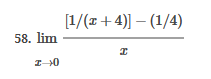
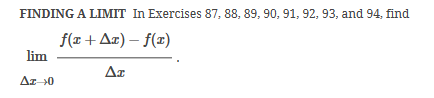
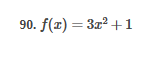

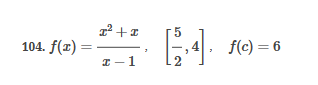

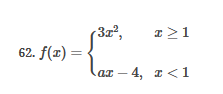
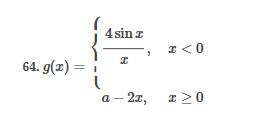



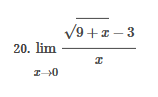
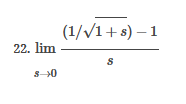
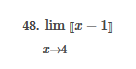
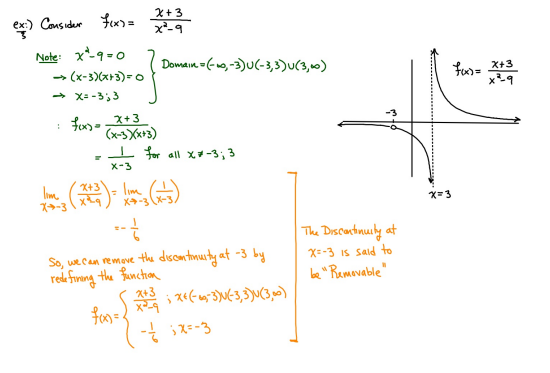
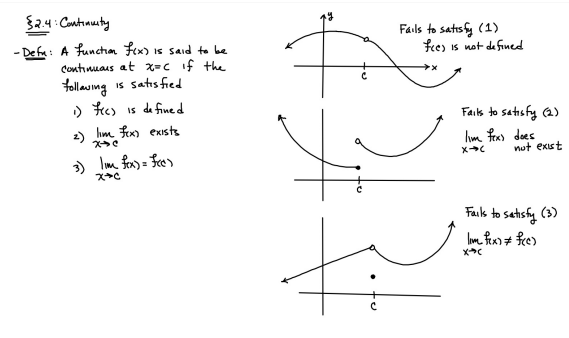
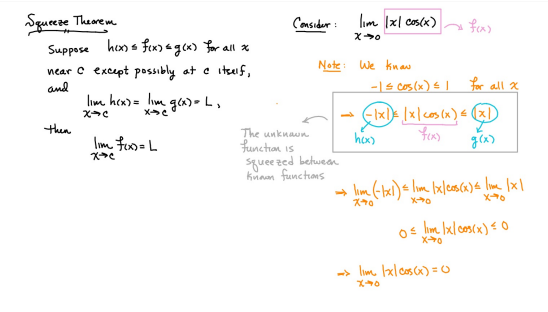
ex: ) lim As X-8 , X-8- (x-8) M F(x)- Note: Let Fix) = (x-8) really small # : X= 8 is a Vertical Asymptote - either - f(x ) - ( really large neg . # ) f - - 60 as x -+ 8 X or : lim e = - 60 f - to as x - 8- X-8 ( x-8) To determine which one consider the following. X X- 850 when X 8 So It x-8", x-870 and 8 f - really small pos . #$2.5: Infinite Limits ex: ) Evaluate lim 6x*+ X-1 ex:) Find the vertical asymptotes 4x -4x- 3 on the graph of 4x"+4x -24 x - ax ax +18x lim (3x - 1 )2x + 1 ) approach x= - Frome (axti ) (2x-3) 4 ( x * + *-6) the right *3(x-2)-9x(x-2) 3x - 1 2x - 3 4 ( x+ 3 ) (x-2 ) ( x-2)[x3 - 9x ] 3 (-4)-1 4(x+3 )(x-2 ) 2(-1)-3 x (x-1) (x - 9 ) - 4 (x# 3)(x-2) x(x-a)(x-3)(x+3) -1- 3 4 Find the values of x that cause the simplified * (x- 3) function to be undefined - Vertical Asymptotes are X=0 and x=3Theorem : Intermediate Value Theorem (IVT) ex: ) Prove that If : for=x"- 2- cos(x ) i) $ is continuous on the interval [ a, 6] has at least one zero on the iis fras # f(b) interval [o, or] and k is any value between fra) and feb). (i) y=x"-2 is a polynomial so if is then there exists some value ce (a, b ) such that continuous everywhere fees = k yo cos ( x) is a continuous trignometric Function Since f is the difference of continuous functions , it is continuous (ii) fea) = fcos f(b)= f(m) = -2-1 - T-2+1 Trox fit) =-3 >0 Since O lies between flo's and fCT) there must exist some value ce ( ofT ) such that frey = 0ex ) Consider Foxy= X+3 x2-9 Note: X"- 9=0 - (x-3)(x13) =0 Domain = (-10,-3)U(-3, 3)(3, 0) for= *+3 - X:-3;3 X 1- 9 : for= 2+3 -3 (x-3 ) (x+3) for all X #- 3; 3 X -3 X-3 X4-3 *=3 The Discontinuity at So, we can remove the discontinuity at -3 by X= -3 is said to redefining the function be " Purmovable" *+ 3 *-_qi x*(-6- 3)N(-3, 3) ( 3, 00 ) 7 3x =- 3$2.4: Continuity Fails to satisfy ( 1) - Defu: A function Fix) is said to be fees is not defined continuous at x=c if the following is satisfied C 1) fees is defined Fails to satisfy (2) 2 ) home fox's exists lime fox's does not exist 3) love foxy = fees Fails to satisfy (3 )Squeeze Theorem Consider : lim [x/ cos(x ) Suppose hos fixs= goes for all * near C except possibly at e itouf, Note: We know and - 1 = cos ( x ) = | for all x x / then Ime Fox = L The unknown fixs Function Is 9 (x ) squeezed between Kinnon functions him (- 1x1 ) = him (x/ cos(x)= lume /x1 Of him / x/cos( x ) = 0 -> hi lal cos ( x ) = 0ex. ) lim "- 1) : of the indeterminate X e - l form The irrational number e = 4 12 K E -1 e = lim (1+ x ) ax = 4 Imm (e"+1) e - = (ex ) - 1 ~2.71828... = 4 (e+ 1 ) Difference = 2 of Squares$2.3 Continued Great geometric proof cose tame of this in the textbook Special Limits 9 SIMO Note : tan On 9 Sie Tim (1+ x) " Definition of the Cos B cos e = e irrational number e 9-0 SMO ex ) lom sin(x) (1- costs X-0 = 1 lim sin(4x ) lim 5 m (x ) ex: ) X X-70 sm(5x ) SINCE = lim ( sun(4x) ) ( sin(5x) X : 1.0 Now In the :0 special limit 14 x Sin(4% 5x SIn( 5x) 5% sm(4x = lim141-2 54. lim I - 3\fFINDING A LIMIT In Exercises 87, 88, 89, 90, 91, 92, 93, and 94, find f(I + Ax) - f(I) lim AT Ar-10\fUSING THE MERLEDLA'IE 1VALUE THEOREM PP in Exercises 99, 100, 101,102, 103, and 104, verify that the Intermediate TJalue Theorem applies to the indicated interval and nd the value of r: guaranteed by the theorem. 104. [,.4 . f(c ) = 6\fT. 62. HE4 sinc 64. gI a - 20,EHSTENEE OF A ZERO In Exercises 83, B4, 35, SE, 8?, and 83, explain why the function has at least one zero in the given interval. 88. Function Interval g(t) = (+ + 2t - 2) In(t? + 4) [0, 1]1+8 1 22. lim
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


