The details of the solution steps as a dynamic programming algorithm is given as follows:

1. Define the problem in stages and states: In this problem, the stages are the months and the states are the starting inventory levels for each month. Thus the firm can enter any month with any inventory level ranging from zero to the inventory limit. Each level is a separate state that affects decisions.

2. Find a recursive formula: Define a recursive formula that connects the decisions made in the previous stage (for each state) to the next stage.

3. Start from the last period and go back to the beginning: Since there is no later stage to effect decisions, it is easy to find optimal decisions at any given state for the last month. For example, at last stage (month), if your demand is 40 units and you have 40 products in your inventory at the start of the month, you manufacture none. However, if you have 35 units in your inventory at the start of the last month, you need to manufacture 5 units during that month. Once you calculate states for the last stage, you need to go backwards one month at a time to the beginning by using a recursive formula, which will connect last months decisions to the previous month's. Once you reach the starting month, you will find the optimal solution easily since you would have connected all previous decisions to the states of the first month. This way, you will arrive at the minimum overall cost.

   For product A, the demand during the next four months has been forecasted as follows:

Month	Units Required
1	1
2	3
3	2
4	4

the start of a month, the firm needs to decide the number of units to be produced in the current month. The following are the costs involved:

• Fixed cost: Irrespective of the number of units produced, a fixed cost of $3 is incurred for setup (as long as at least one unit is manufactured).
• Variable cost: A variable cost of $1 is incurred for each unit manufactured.
• Inventory cost: An inventory cost of 50 per unit on hand is incurred at the end of each month.

Further, the manufacturing limit is 5 units for a month and inventory limit is 4 units.

To determine a production schedule that will meet all demands on time and will minimize the sum of production and inventory costs during the four months, the following steps are followed:

4. Stages and states: The stages are 4 (since there are 4 months to plan for), and the states are the possible starting inventory levels, which can be 0, 1, 2, 3, or 4 (since the inventory limit is 4).
5. The recursive formula: Except for the last month, a recursive formula can be defined as follows for month i:

Cost(Starting inventory) = Cost of Production + Inventory cost(Ending inventory) + Costi+1(Ending inventory)

6. Start from the last period and go back to the beginning: For the last month, depending on the starting inventory level, the following costs will be incurred:

   • Cost₄(0) = 3 + 4 x1 = 7
   • Cost₄(1) = 3 + 3 x1 = 6
   • Cost₄(2) = 3 + 2 x1 = 5
   • Cost₄(3) = 3 + 1 x1 = 4
   • Cost₄(4) = 0 = 0

For month 3, with a starting inventory level of 2, the following recursive formula will apply:

thus:

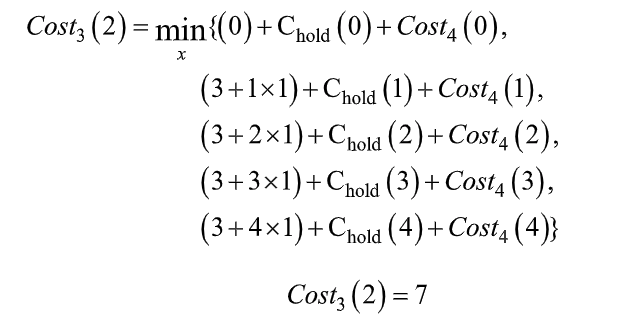
Here, C pro is the production cost, C hold is the inventory cost for any product that is not sold at the end of the month and the Cost 4 is the cost of entering month 4 with the inventory level (which you can get from the previous set of equations).

This problem has a runtime complexity of O(5ⁿ) due to the number of possible states. Each node in the recursion tree will need to compare 5 new nodes, as shown in the following figure. The value of each state needs to be calculated repetitively.

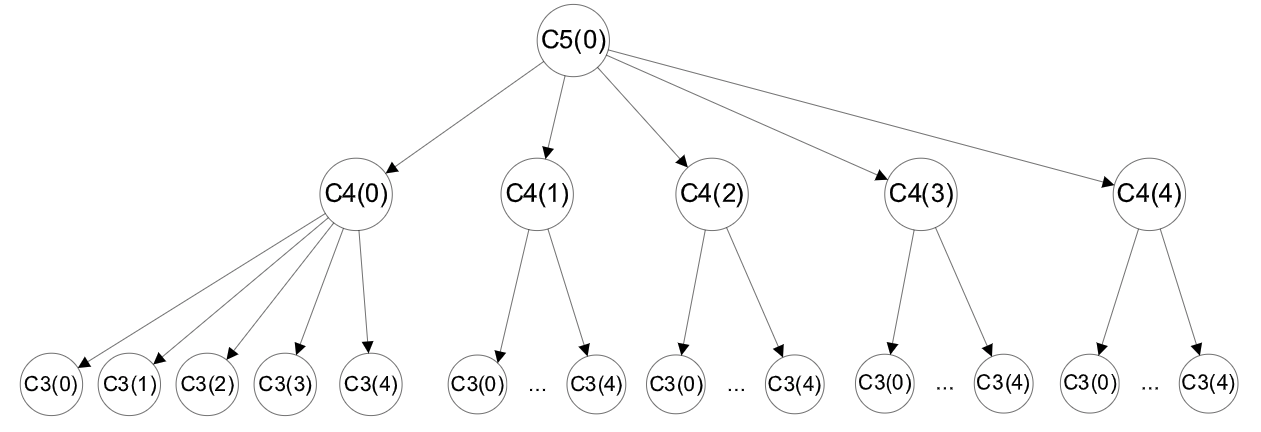
^{Figure 1: Recursion tree}

• For easy readability, use full variable names instead of short 2-3 character abbreviation.
• For code reusability, develop separate methods when available.

Before you begin, observe the existing data structure in InventoryAndManufacturingPlan.java and develop constructors, getters, and setters (if necessary). There are two memorization variables:

private double[][] memoriseCostOfStates;

private int[][] memoriseProductionOfStates;

Task

Develop the planProduction() method as the main method. Consider the 3 cases below:

1. Last stage/month
2. Intermediate stages/months
3. First stage/month

1

Use the two memorization variables to store the calculated minimum cost and optimal production amount for each state of a month. After calculating all the way down to the first month, select the strategy that gives the minimum total cost from the first month and go through each month sequentially to find out the optimal production and optimal inventory levels for each month. Store these values in private int[] productionPlan and private int[] inventoryPlan variables, respectively.

Task

Develop the productionCost(int amountOfProduction) method to find the costs incurred in the last month.

Remember that if the firm does not manufacture any products, then no cost is incurred, but if they manufacture any amount of product, they incur a fixed cost and a variable cost per unit of product manufactured.

Task

Develop the totalCost(int startingInventory, int planningPeriod) method to calculate the cost during the intermediate and first months.

For these months, they need a recursive calling to the total cost to achieve already calculated cost of (next) months. Do not forget to check and return the value if it is already calculated and stored in memorization variables. While calculating the states, ensure that the inventory or production levels are not exceeded. To achieve this, first calculate and limit the states of the month to possible inventory and production level pairs. Since the starting inventory level is given to the function as a parameter, limit the minimum and maximum amount of production for the month.

InventoryAndManufacturingPlan.java

public class InventoryAndManufacturingPlan { private int numberOfPeriods; // planning period private double inventoryHoldingCostPerProduct; private double manufacturingCostPerProduct; private double setUpCostPerPeriodOfManufacture; private int productionCapacity; // limit of production per period private int inventoryCapacity; // limit of production per period capacity private int[] productionPlan; private int[] inventoryPlan; private int[] demands; /* * row are starting inventory amounts columns are periods * and values are costs */ private double[][] memoriseCostOfStates; /* * row are starting inventory amounts columns are periods and values are production amounts */ private int[][] memoriseProductionOfStates; /** * @param inventoryHoldingCostPerProduct * @param manufacturingCostPerProduct * @param setUpCostPerPeriodOfManufacture * @param productionCapacity * @param inventoryCapacity * @param demands market demand per period and index 0 must be undefined (-1), * values should start from index 1 */ public InventoryAndManufacturingPlan(double inventoryHoldingCostPerProduct, double manufacturingCostPerProduct, double setUpCostPerPeriodOfManufacture, int productionCapacity, int inventoryCapacity, int[] demands) { super();

} public int[] getProductionPlan() { return null; }

public void setProductionPlan(int[] productionPlan) {

}

public int[] getInventoryPlan() { return null; }

public void setInventoryPlan(int[] inventoryPlan) { } public double[][] getMemoriseCostOfStates() { return null; }

public int[][] getMemoriseProductionOfStates() { return null; } /** * */ public void planProduction() { //Case 1: last period //Case 2 intermediate periods; periods except first and last //for each period //for each starting inventory level

//total cost will be production, production setup and inventory

//Case 3 first period (index 1); starting inventory is 0 so different /* * find and write optimal */ //get optimal for first period and calculate inventory

//for the remaining periods

//get previous excess inventory

}

public double productionCost(int amountOfProduction) {

return -1; }

public double totalCost(int startingInventory, int planningPeriod) { //check if it is already calculated

//find min production amount to max production amount

//are we manufacturing ?

//calculate cost

//assign if min cost

return -1; }

public static void main(String[] args) { /* * This main method is a stub. * It does nothing. * Feel free to write your own code to test your implementation. * In this case, we have nothing actionable in here, just this comment block, so the JVM should rapidly lose interest and move on to the rest of your code. */ } }

Your company noticed that the API you developed is only applicable to a few companies, but if it is generalized, it can be sold to many other firms. Therefore, you have been tasked with developing a new API that takes in more details such as costs and limits, which should be adjustable for different periods, and does not contain a period limit. In this version, the user should be able to define a starting inventory level and ending inventory level for the duration of the planning period.

Your company believes that this will be more useful because during different months of the year, demand and production costs change (especially due to the changing energy and raw material costs). Since companies have a limited production capacity, they need to manufacture at full capacity when the manufacturing cost is low and store it for sale during months when the demand for the product exceeds the manufacturing capacity.

Comments

Costz (2) = min{Cpro (produced )+Chola (ending inventory) + Costa (ending inventory)} ending inventory = demandz - starting inventoryz - producedz Costz (2)= min{(0) + Chola (0) + Costa (0), (3+11)+Chold (1) + Costa (1), (3+2x1) + Chola (2)+Costa (2), (3+3x1) + Chold (3)+ Costa (3), (3+4x1) + Chold (4)+ Costa (4)} Costz (2) = 7 C5(0) CA(0) (CA(2) C4(3) C4(4) | our ord or c) 4) ( 0) (1). C3(0) [C3(4) Costz (2) = min{Cpro (produced )+Chola (ending inventory) + Costa (ending inventory)} ending inventory = demandz - starting inventoryz - producedz Costz (2)= min{(0) + Chola (0) + Costa (0), (3+11)+Chold (1) + Costa (1), (3+2x1) + Chola (2)+Costa (2), (3+3x1) + Chold (3)+ Costa (3), (3+4x1) + Chold (4)+ Costa (4)} Costz (2) = 7 C5(0) CA(0) (CA(2) C4(3) C4(4) | our ord or c) 4) ( 0) (1). C3(0) [C3(4)