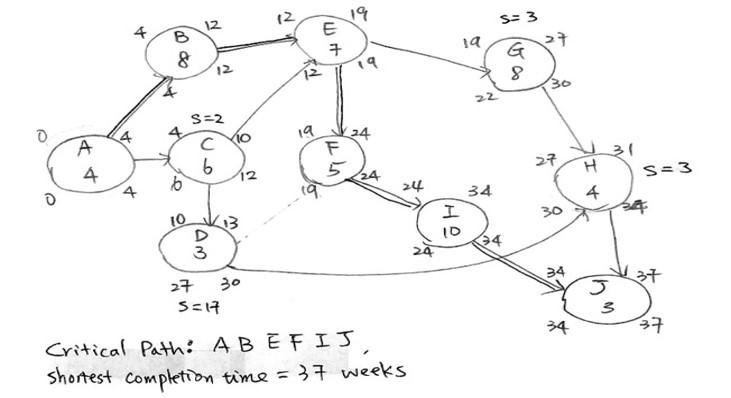
Question: The following activity table has had its project network done. At its normal activity time, the shortest critical path has a finish time of 37
The following activity table has had its project network done. At its normal activity time, the shortest critical path has a finish time of 37 weeks [See the figure]. The table provides you a normal activity time and its normal activity cost. It also provides you a shortest finish time and a higher cost for crashing that activity. What is the best way to crash the project such that it can be finished in 32 weeks? How much is the extra crashing cost on top of the normal activity cost for this crashing plan? Please provide the sequence of your crashing plan.
| Activity | Normal Time (in weeks) | Immediate Predecessor | Crash Time (in weeks) | Total Normal Cost | Total Crash Cost |
| A | 4 | - | 4 | $2,000 | $2,000 |
| B | 8 | A | 7 | $6,200 | $7,800 |
| C | 6 | A | 4 | $4,500 | $6,500 |
| D | 3 | C | 2 | $3,300 | $4,800 |
| E | 7 | B,C | 6 | $5,300 | $6,200 |
| F | 5 | E | 3 | $3,000 | $3,800 |
| G | 8 | E | 5 | $6,400 | $9,100 |
| H | 4 | D,G | 2 | $2,200 | $3,000 |
| I | 10 | F | 6 | $10,500 | $14,500 |
| J | 3 | I,H | 3 | $4,500 | $4,500 |
1
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


