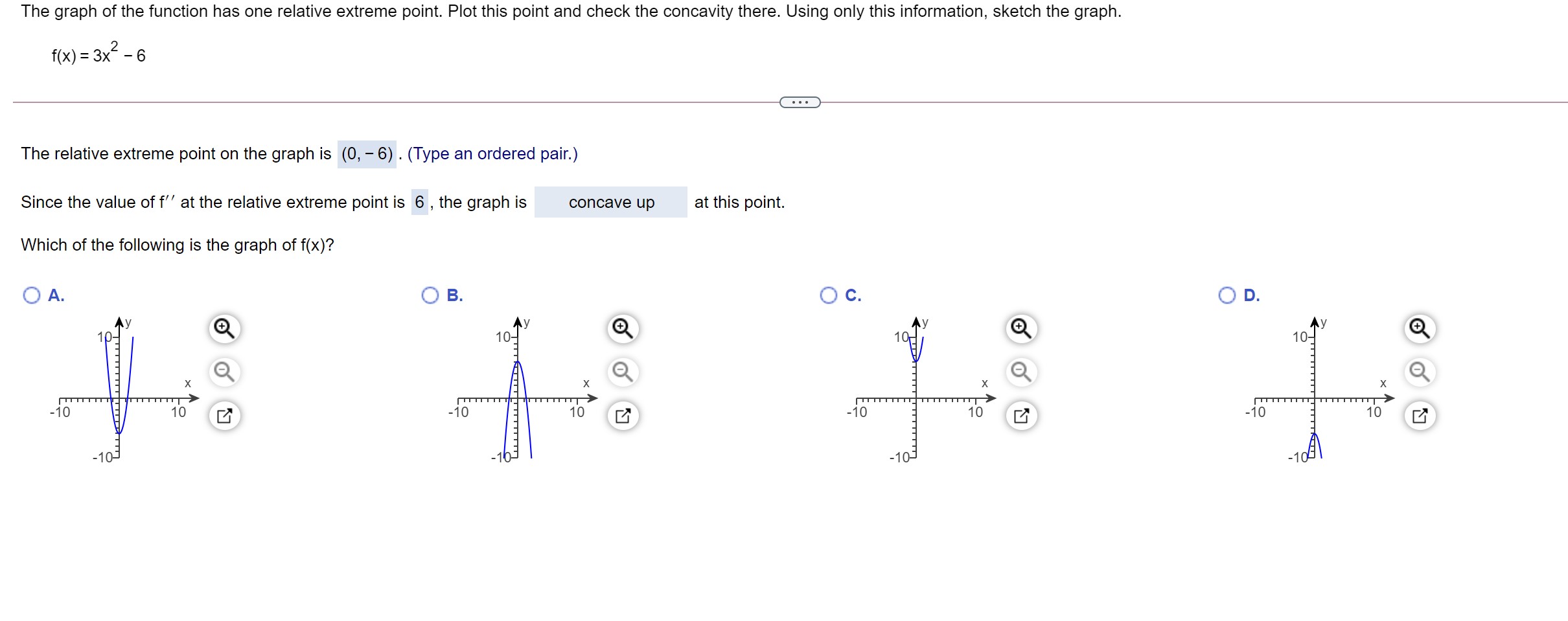
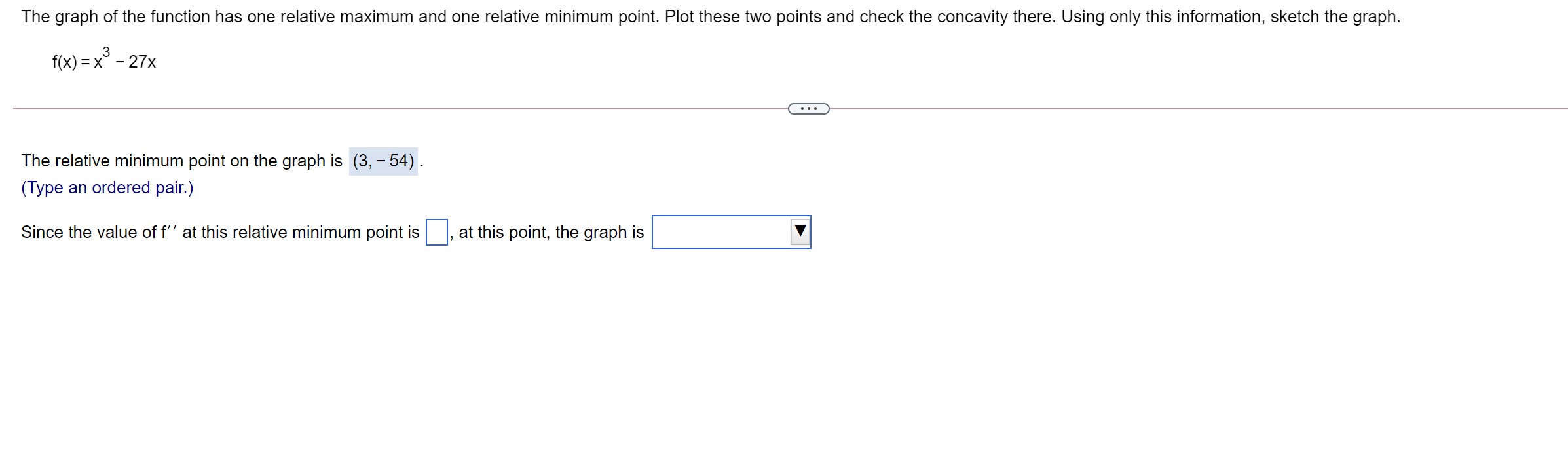
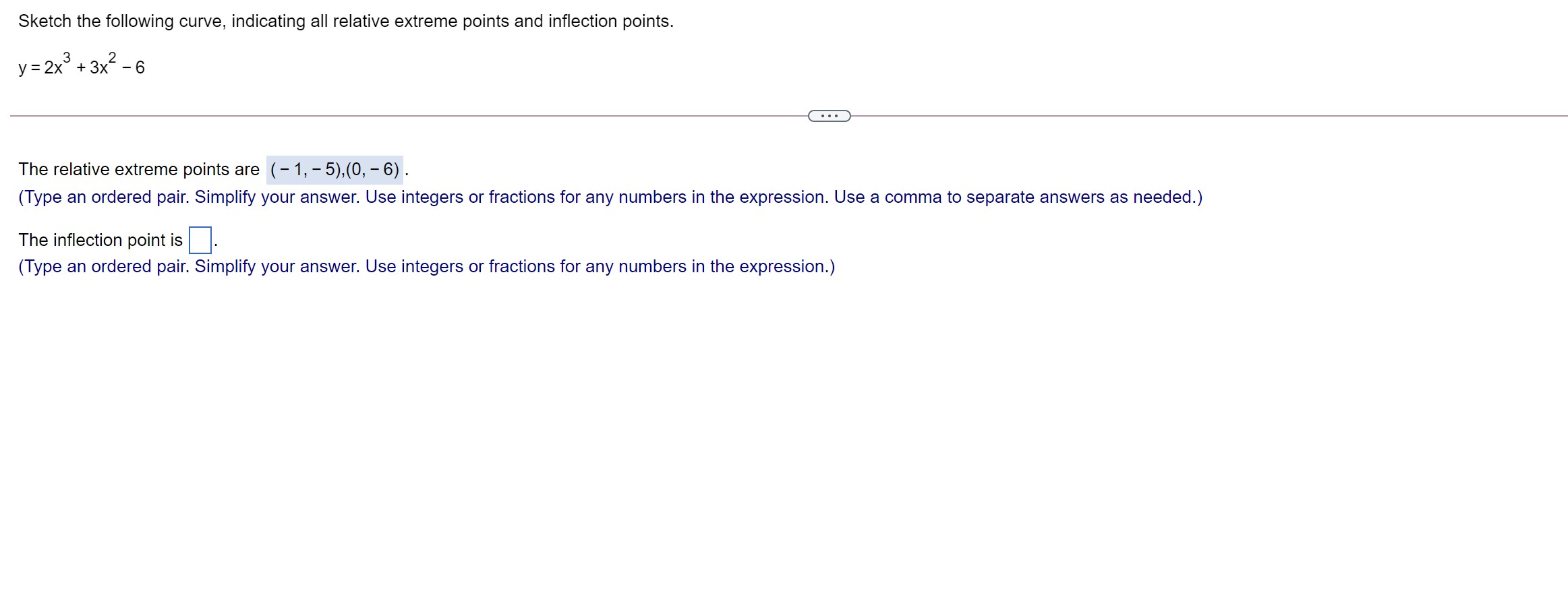
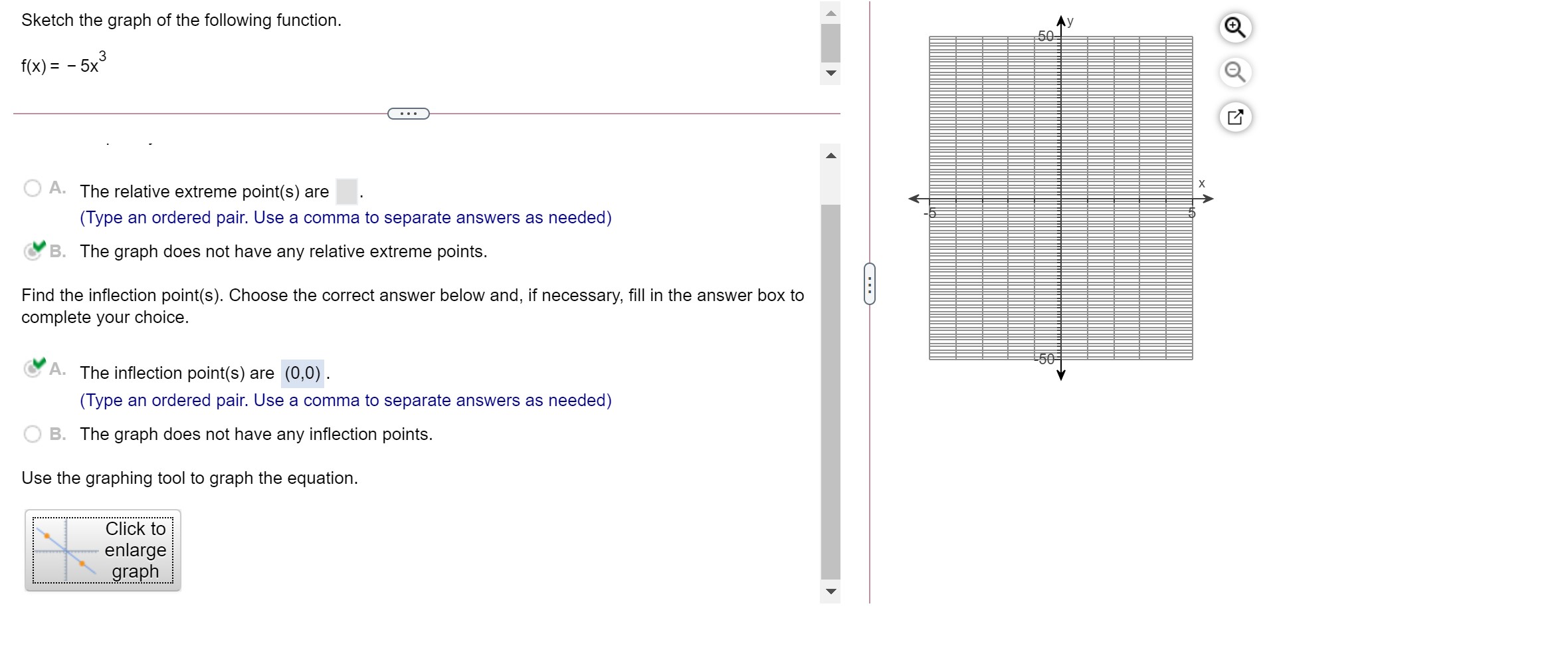
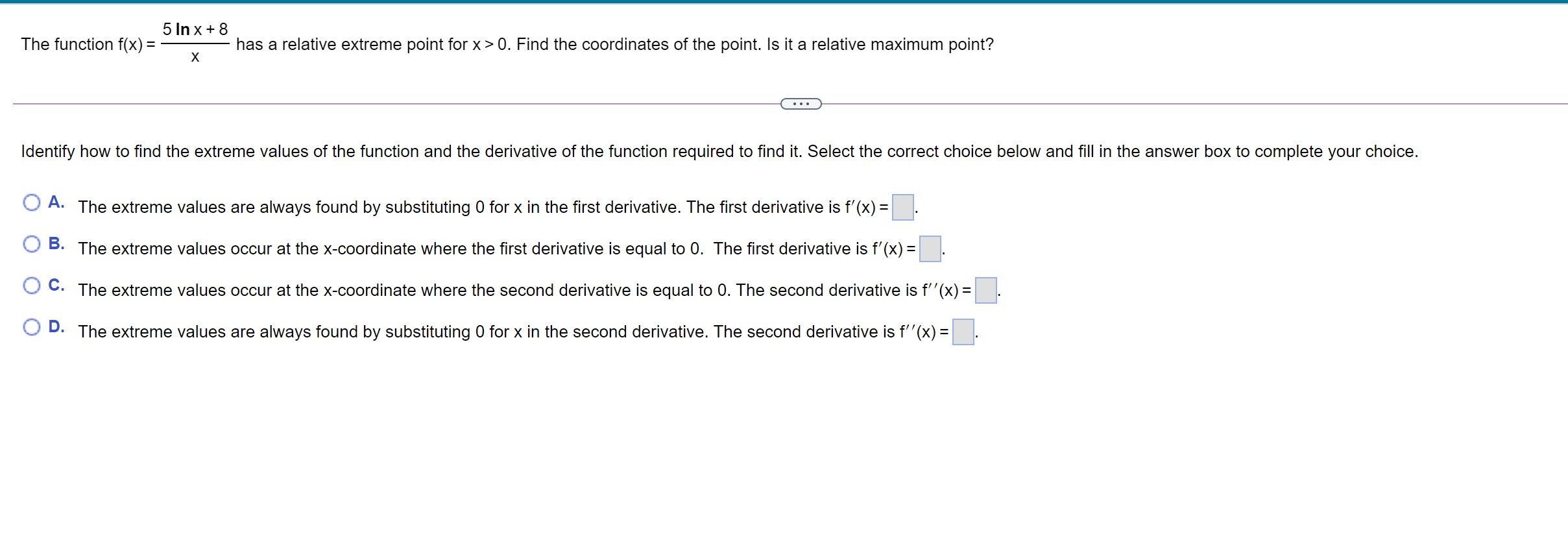
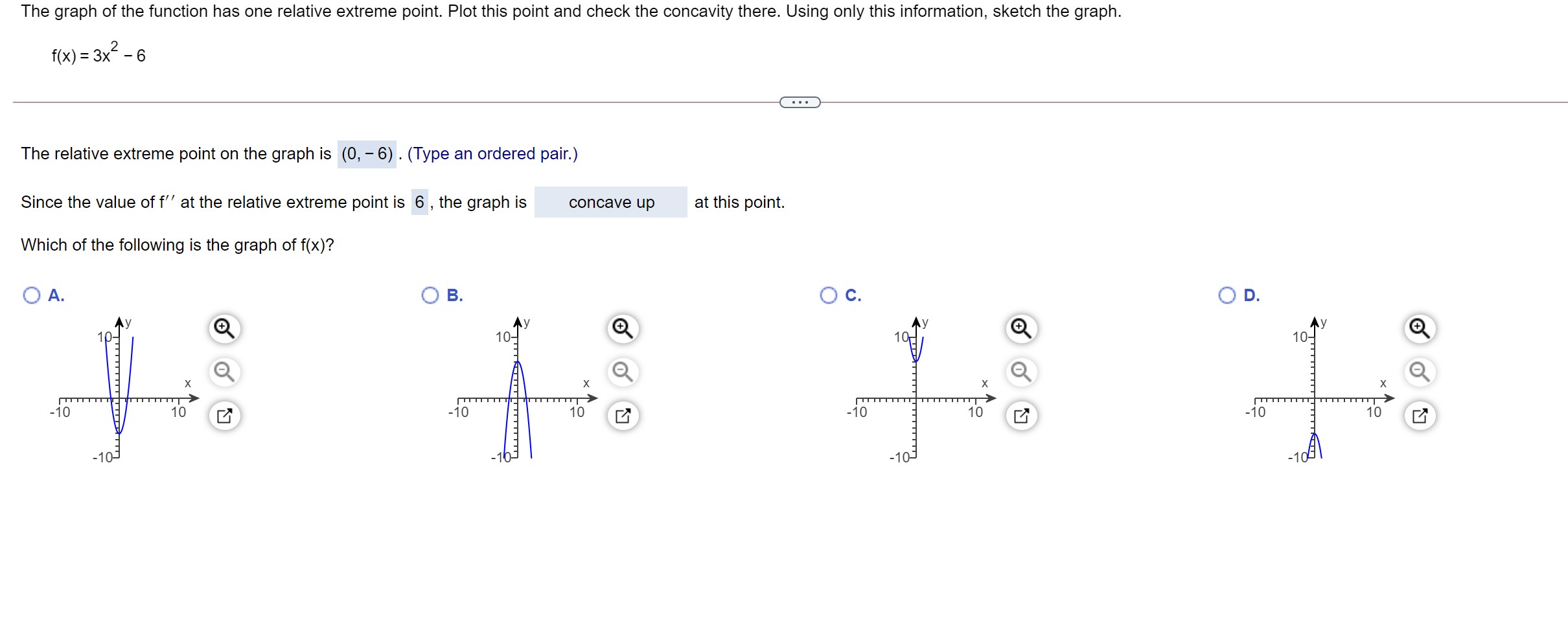
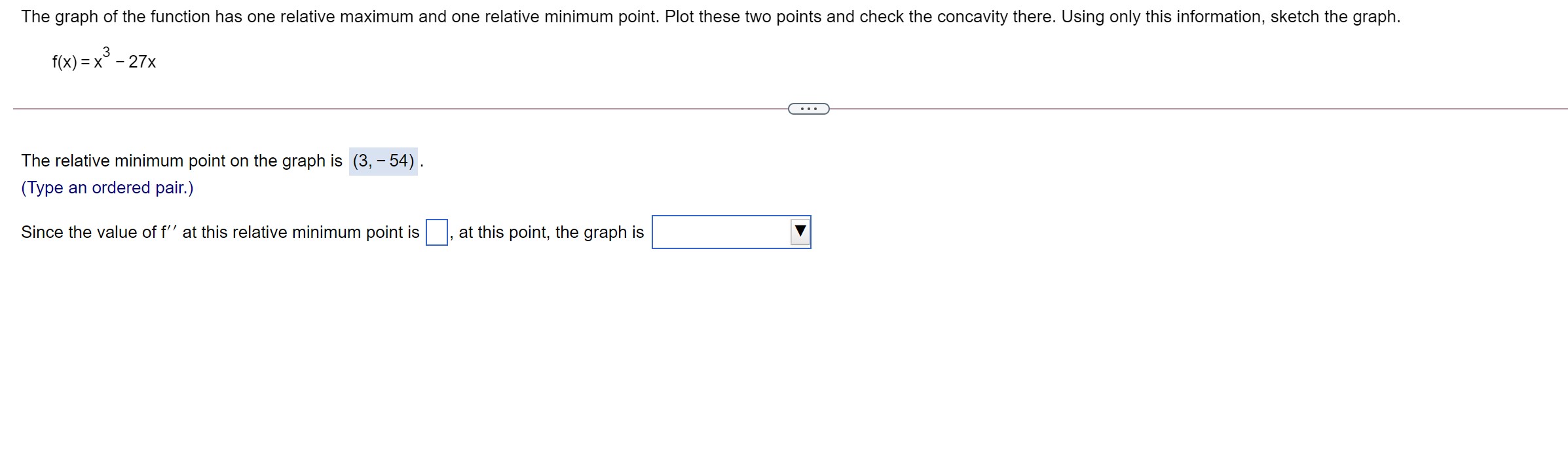
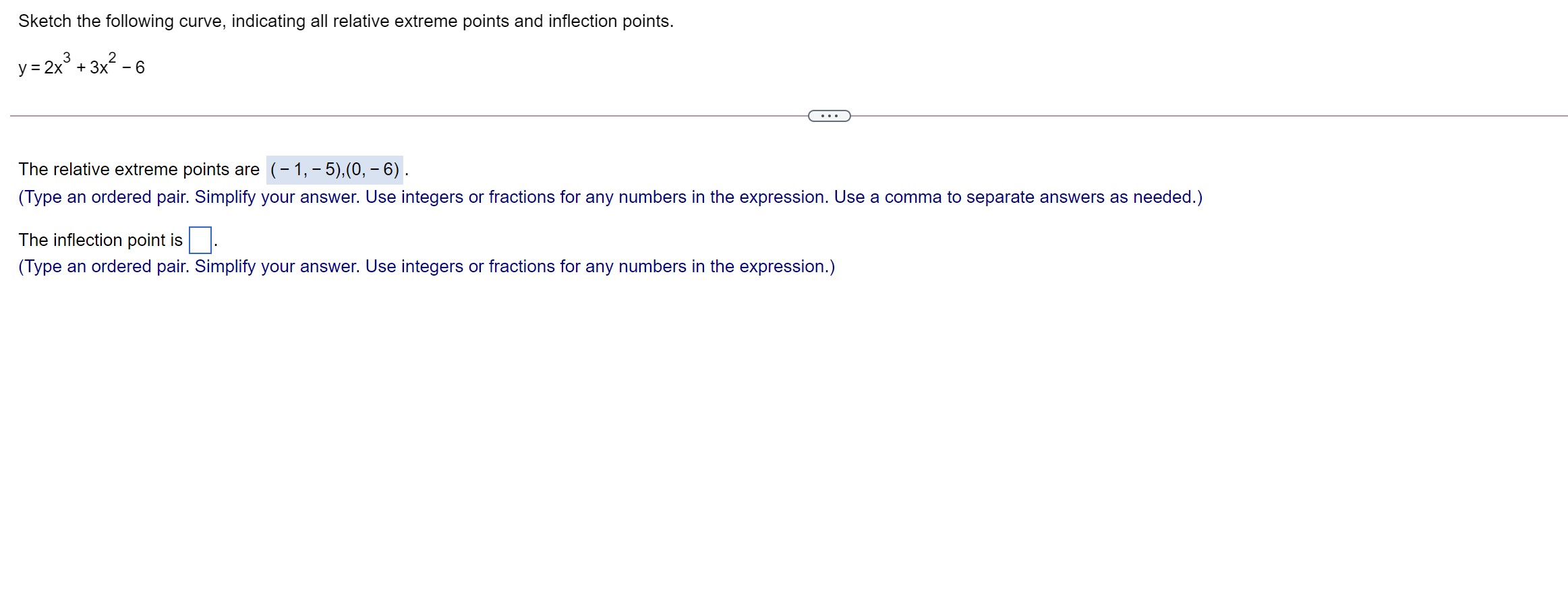
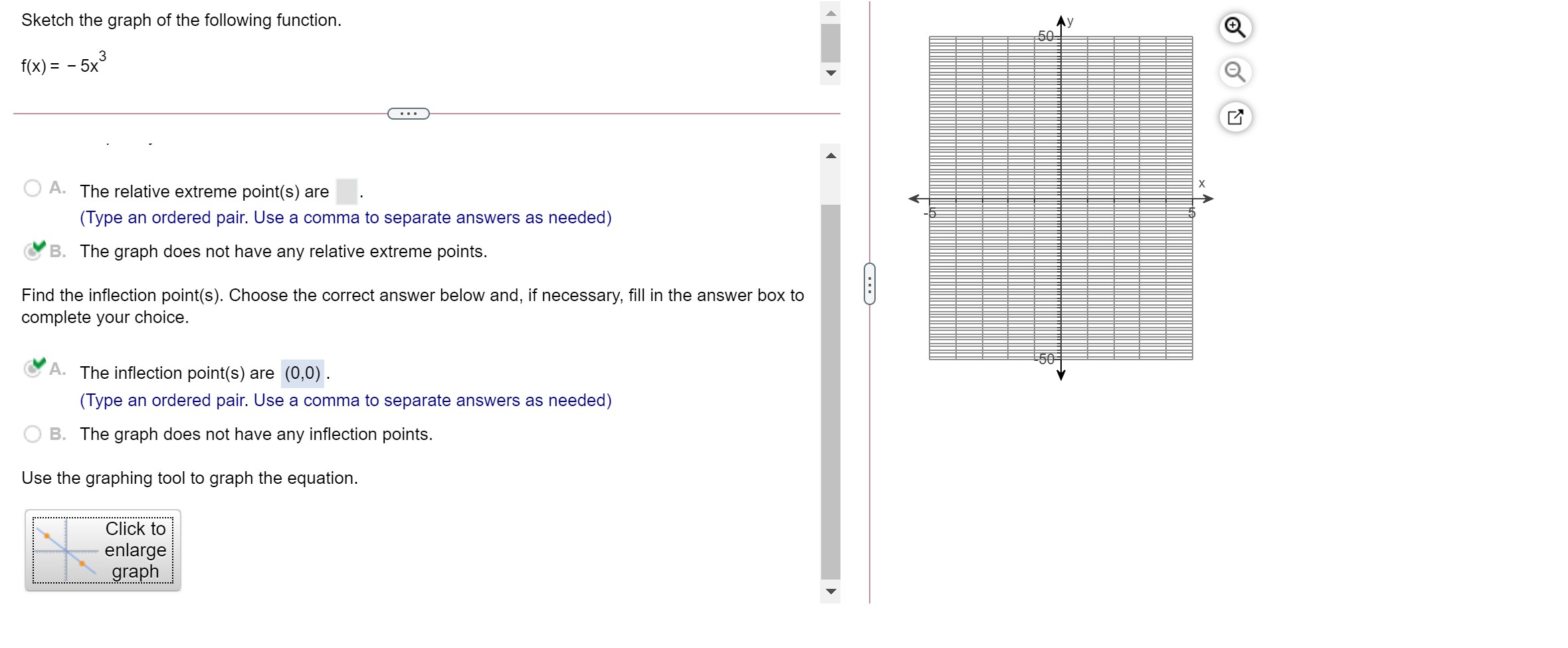
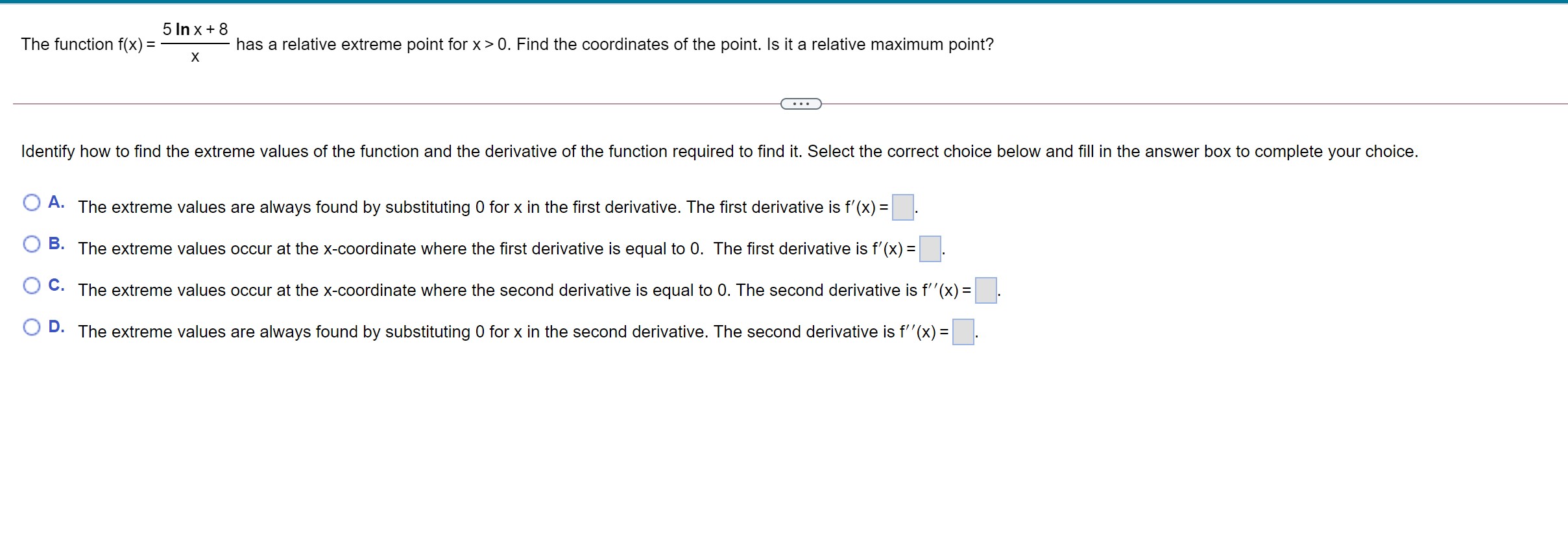
The graph of the function has one relative extreme point. Plot this point and check the concavity there. Using only this information, sketch the graph. f(x) = 3x2 , e The relative extreme point on the graph is (0, 6) . (Type an ordered pair.) Since the value of f\" at the relative extreme point is 6 , the graph is concave up at this point. Which of the following is the graph of f(x)? OA. The graph of the function has one relative maximum and one relative minimum point. Plot these two points and check the concavity there. Using only this information, sketch the graph. f(x) = x3 27x The relative minimum point on the graph is (3, - 54) . (Type an ordered pair.) Since the value of f\" at this relative minimum point is , at this point, the graph is V Sketch the following curve, indicating all relative extreme points and inflection points. y= x5 - 3x + 5. . . . Find the first derivative of y. y' = 3x - 3 The relative extreme points are ( - 1,7), (1,3) . (Type an ordered pair. Use a comma to separate answers as needed.) . . . The inflection points are (Type an ordered pair. Use a comma to separate answers as needed)Sketch the following curve, indicating all relative extreme points and inection points. y=63x2x3 The relative extreme points are (-2,2),(0,6) . (Type an ordered pair' Use a comma to separate answers as needed.) The inection points are . (Type an ordered pair. Use a comma to separate answers as needed.) Sketch the following curve, indicating all relative extreme points and inflection points. y = 2x + 3x2 - 6 The relative extreme points are ( - 1, - 5),(0, -6) . (Type an ordered pair. Simplify your answer. Use integers or fractions for any numbers in the expression. Use a comma to separate answers as needed.) The inflection point is. (Type an ordered pair. Simplify your answer. Use integers or fractions for any numbers in the expression.)Sketch the graph of the following function. 50 f (x ) = - 5x5 O A. The relative extreme point(s) are X (Type an ordered pair. Use a comma to separate answers as needed) B. The graph does not have any relative extreme points. Find the inflection point(s). Choose the correct answer below and, if necessary, fill in the answer box to complete your choice. A. The inflection point(s) are (0,0) . (Type an ordered pair. Use a comma to separate answers as needed) O B. The graph does not have any inflection points. Use the graphing tool to graph the equation. Click to enlarge graph5 In x + 8 The function f(X) = X - has a relative extreme point for x > 0. Find the coordinates of the point. Is it a relative maximum point? Identify how to find the extreme values of the function and the derivative of the function required to find it. Select the correct choice below and fill in the answer box to complete your choice. O A. The extreme values are always found by substituting 0 for x in the first derivative. The first derivative is f'(x) =. O B. The extreme values occur at the x-coordinate where the first derivative is equal to 0. The first derivative is f'(x) = O C. The extreme values occur at the x-coordinate where the second derivative is equal to 0. The second derivative is f"(x) = O D. The extreme values are always found by substituting 0 for x in the second derivative. The second derivative is f'(x) =