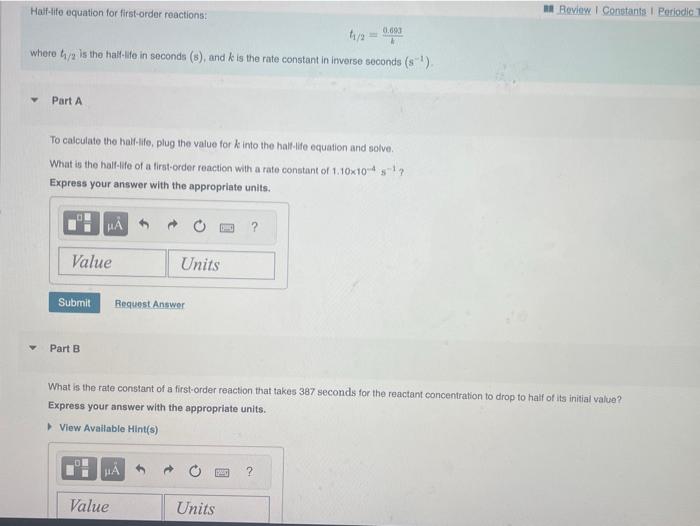
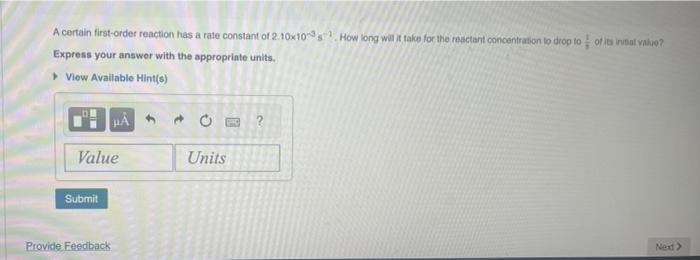
The integrated rate law allows chemists to predict the reactant concentration after a certain amount of time, or the time it would take for a certain concentration to be reached. The integrated rate law for a first-order reaction is: [A]=[A]0ekt Now say we are particularly interested in the time it would take for the concentration to become one-half of its initial value. Then we could substitute 2[A]0 for [A] and rearrange the equation to: t1/2=k0.693 This equation calculates the time required for the reactant concentration to drop to half its initial value. In other words, it calculates the half-life. t1/2=h0.693 where h1/2 is the hall-lfe in seconds (s), and k is the rate constant in inverse seconds (s1). Part A To calculate the half-life, plug the value for k into the halt-life equation and solve. What is the half-life of a first-order reaction with a rate constant of 1.10104s1 ? Express your answer with the appropriate units. Part B What is the rate constant of a first-order reaction that takes 387 seconds for the reactant concentration to drop to haif of its initial value? Express your answer with the appropriate units. A certain first-order reaction has a rate constant of 2.10103s1. How long wili t take for the reactant concentrabon to drop to 71 of is inisat value? Express your answer with the appropriate units