The moon Phobos moves around the planet Mars in a circular orbit.

$($a$)$ Outline why the gravitational force does no work on Phobos.

$(1)$

The orbital period $T$ of a moon orbiting a planet of mass $M$ is given by:

$\frac{R^3}{T^2}=kM$

where $R$ is the average distance between the center of the planet and the center of the moon.

$($b$)$ Show that $k=\frac{G}{4{}^2}.$

$(3)$

The following data for the Mars$-$Phobos system and the Earth$-$Moon system are available:

Mass of Earth $=5\mathrm{.}97{10}^{24}kg$

The Earth$-$Moon distance is $41$ times the Mars$-$Phobos distance.

The orbital period of the Moon is $86$ times the orbital period of Phobos.

$($c$)$ Calculate, in kg$,$ the mass of Mars.

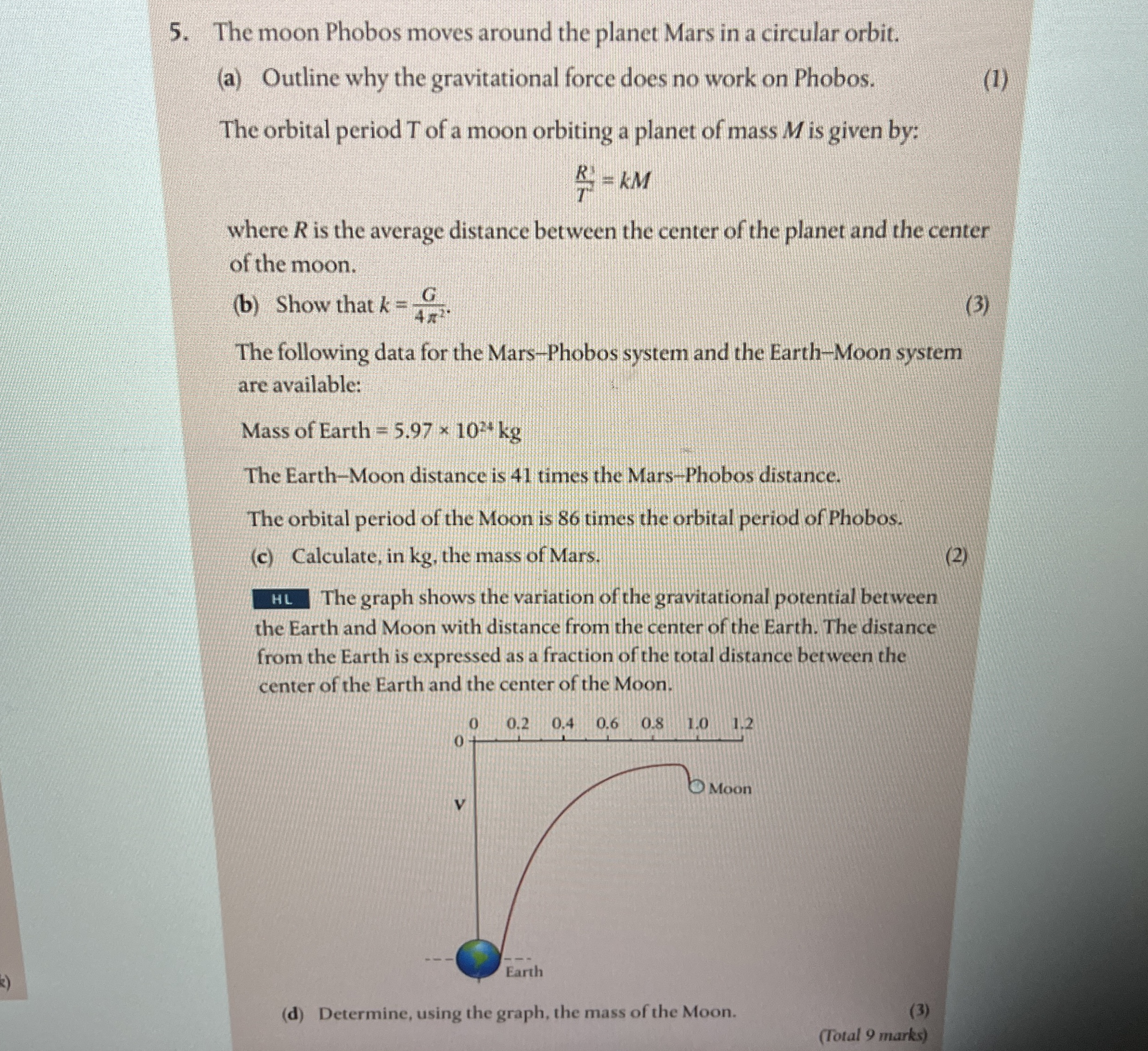
$$ The graph shows the variation of the gravitational potential between the Earth and Moon with distance from the center of the Earth. The distance from the Earth is expressed as a fraction of the total distance between the center of the Earth and the center of the Moon.

$($d$)$ Determine, using the graph, the mass of the Moon.

$(3)$

$($Total $9$ marks$)$