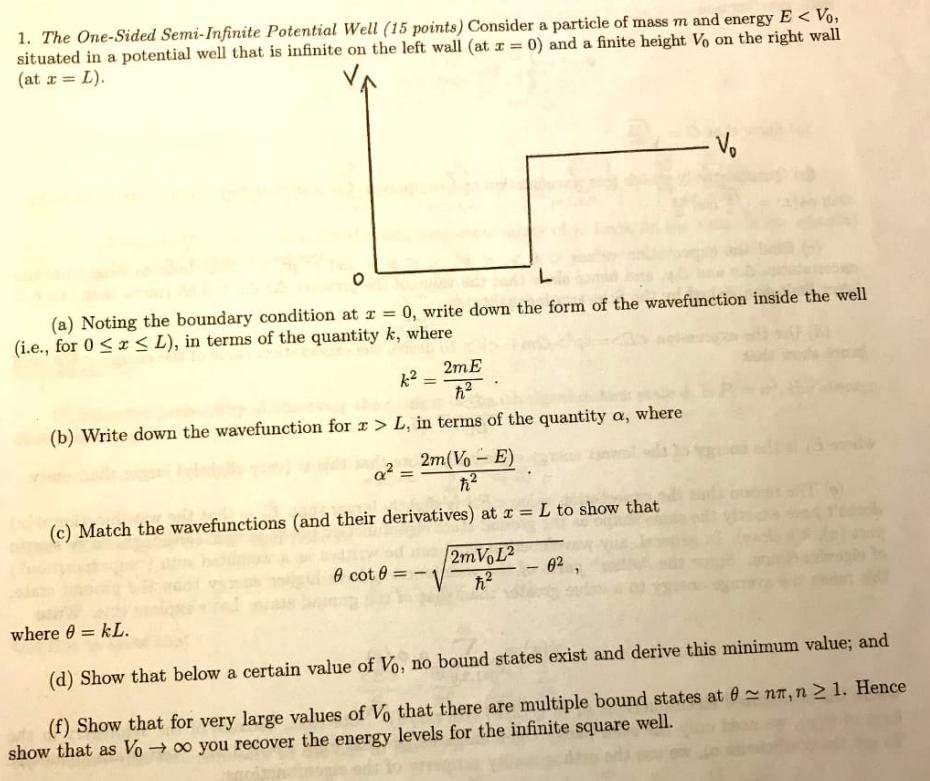
The One-Sided Semi-Infinite Potential Well (15 points) Consider a particle of mass m and energy E < Vo, situated in a potential well that is infinite on the left wall (at x = 0) and a finite height Vo on the right wall (at x = L). O = 0, write down the form of the wavefunction inside the well (a) Noting the boundary condition at x = (i.e., for 0x L), in terms of the quantity k, where k = 2mE (b) Write down the wavefunction for > L, in terms of the quantity a, where 2m(VoE) (c) Match the wavefunctions (and their derivatives) at x = L to show that = 0 cot 0 = =- 2mVoL2 - Vo - 0, where 0 = KL. (d) Show that below a certain value of Vo, no bound states exist and derive this minimum value; and (f) Show that for very large values of Vo that there are multiple bound states at 0nn, n 1. Hence show that as Voo you recover the energy levels for the infinite square well.