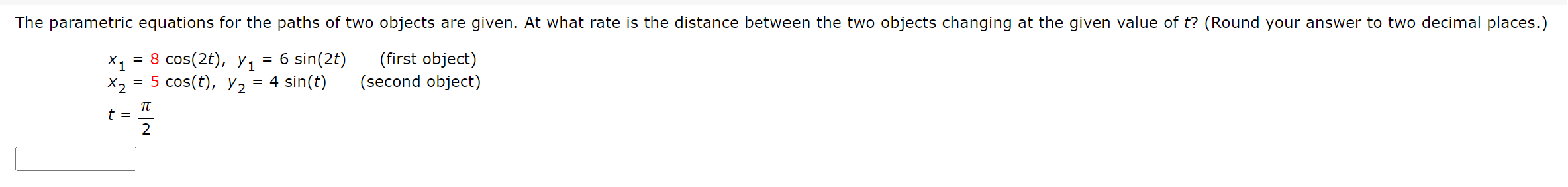
The parametric equations for the paths of two objects are given. At what rate is the distance between the two objects changing at the given value of t? (Round your answer to two decimal places.) X = I = 8 cos(2t), y, = 6 sin(2t) (first object) 5 cos(t), y, =4 sin(t) (second object) X N I r., it NS Find a unit normal vector to the surface at the given point. [Hint: Normalize the gradient vector VF(x, y, z).] Surface Point ' 3 sin(x y) 9z = 14 (1, E, - ) Find the angle of inclination @ (in degrees) of the tangent plane to the surface at the given point. (Round your answer to two decimal places.) x> +y2=10, (1,3,5) Find a set of parametric equations for the tangent line to the curve of intersection of the surfaces at the given point. (Enter your answers as a comma-separated list of equations. ) z = V x2 + y2, 7x - 3y+ 4z = 29, (3, 4, 5)