The question:

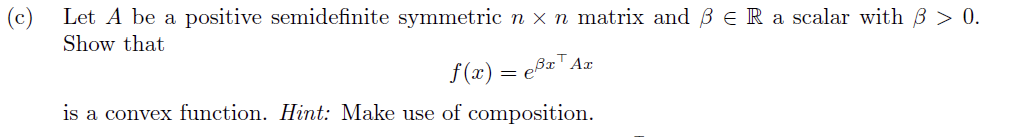
(c) Let A be a positive semidefinite symmetric n x n matrix and B E R a scalar with B > 0. Show that f(a) = eBr Ax is a convex function. Hint: Make use of composition.Problem 3.2: Convexity under Composition LJ Let S g R\" be a nonempty convex set. Let h : S > R be a convex function, and let 5.! : R > R be a monotonically nondecreasing convex function over the set {M3} : a: E S}. Show that the composition function Jet-1*} = g{h.(3:}) is convex. Solution. Let :11: y E S and A E [12}: 1]. Applying the convexity of h and the monotonicity of y, we get lm +[1 My} = 90100? + (1 Mid) g gears) + 1 we (3) S AMMTD + {1 AHMED) (4) = \"(1') + E1 3H3!) which implies that f = g(h{c:)} is convex. The rst inequality [3) follows from the convexity of h. and from the nlonotonicity of g. The second inequality [4} follows from the convexity of g