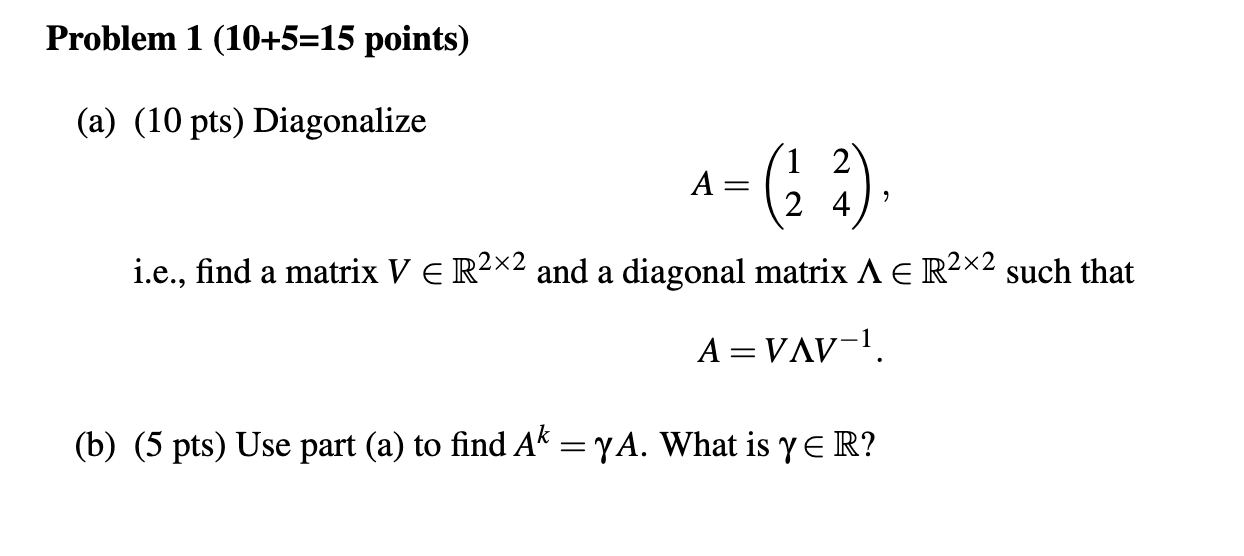
Problem 1 (10+5=15 points) (a) (10 pts) Diagonalize 2 A = 2 4 i.e., find a matrix V E R2x2 and a diagonal matrix A E R2X2 such that A = VAV-1. (b) (5 pts) Use part (a) to find Ak = YA. What is YER?Problem 2 (20 points) We want to find the line y = c1 + cat that best fits the given data: y1 = -1 at time t1 = 0, y2 = 9 at time t2 = 1, and y3 = 1 at time t3 = 2. (a) [10 pts.] Set up and solve the linear least squares problem min, |Ax - b|3. What are A, b and x? (b) [5 pts.] Find a matrix Q with orthonormal columns such that R(A) = R(Q). (c) [5 pts.] Find the orthogonal projection P onto N(AT ).Problem 3 (5+10+7+3 = 25 points) To account for variance in measurement errors one considers weighted least squares problems min |W (Ax - b) 1/2, (1) XERn where W is a diagonal matrix with positive diagonal entries (weights) wii > 0. Measurement with small variance have a larger weight wii- This problem applies the SVD to solve the weighted least squares problem (1) with 0 A = (0 1 0 b = -() and W = 1/2 0 0 (a) (5 pts) Diagonalize WA(WA), i.e., find an orthogonal matrix U E R2X2 and a diagonal matrix A E R2x2 such that WA(WA)I = UAUT. (b) (10 pts) Compute the SVD of WA, i.e., find an orthogonal matrix V E R4X4, and a diagonal matrix E E R2x4 such that WA = UEVT. (c) (7 pts) Find all solutions x E R4 of the weighted linear least squares problem. (d) (3 pts) Find the minimum norm solution of the weighted linear least squares problem.Problem 4 (4+6+10=20 points) Let A E Rmxn, m > n, have an SVD A = UEV' with orthogonal matrix U = (u1, ..., Um) E mxm of left singular vectors, orthogonal matrix V = (v1, . .., Vn) E Rx" of right singular vectors and diagonal matrix E E Rmxn with singular values o1 2 02 2 ... 2 On 2 0. (a) (4 points) Let Q E Rmxm be orthogonal. What are the singular values of QA? Compute an SVD of QA. What are left singular vectors and what are right singular vectors? (b) (6 points) Let t E R. What are the singular values of tA? Compute an SVD of tA. What are left singular vectors and what are right singular vectors? (c) (5 points) Assume that BE RXk, n > k, has an SVD B = VEX' with orthogonal matrix V as before, orthogonal matrix X E RkXk and diagonal matrix E E Rxk with singular values $1 2 52 2 ... 2 Ex 2 0. What are the singular values of AB? Compute an SVD of AB. What are left singular vectors and what are right singular vectors?Problem 5 (20 points, 2 points each) Specify whether the following statement are TRUE or FALSE (no justification necessary). 1) If A is a symmetric n x n matrix with eigenvalues 21, 22, ..., an, then det (A) = 2122...an. 2) Let A be a diagonalizable matrix with eigenvalues 21, ..., an. Then limk . Ak = 0 if and only if |2/|