The question is as follows:

The python code provided is :

## System coefficients

# Total drivetrain inertia, including blades, hub and casted # generator inertia to LSS, [kg m^2] J = 2.15e8; # Damping / friction term [Nm (rad/s)^1] b = 15e6;

## Time vector Tsim = np.arange(0, 100, 0.01)

## Create an integrator variable s = cm.tf([1, 0], [1]) integrator = 1/s

################################################################################ ### Start writing your own code here: ###

# Below, insert and define the variables A, B, C and D. # Change the matrices below to match your answers:

A = [-b/J] B = [1/J] C = [1] D = [0]

# Then, use `cm.feedback`, `cm.series`, and `cm.parallel` and the variable # `integrator` (defined above), to construct the state space system `sys`.

sys1 = cm.series(cm.series(B, cm.feedback(integrator, A)), C) sys2 = cm.parallel(sys1, D)

sys = sys2

### Stop writing your own code here. ### ################################################################################

## Simulation to check if the answer is correct

sys_check = cm.ss(A,B,C,D) y_check, t= cm.step(sys_check,Tsim) y, t= cm.step(sys,Tsim)

plt.figure(); plt.plot(t,y_check,lw=5,ls='-',c='0.6', label='ss-object'); plt.plot(t,y,lw=1,ls='--',c='k', label='constructed sys-object'); plt.legend(); plt.grid(); plt.xlabel('Time [s]'); plt.ylabel('Rotor speed [rad/s]'); plt.title('Step response');

For the life of me I can't figure out how this is supposed to be done and why my answer (given in Italic font) is wrong. Any help is appreciated!

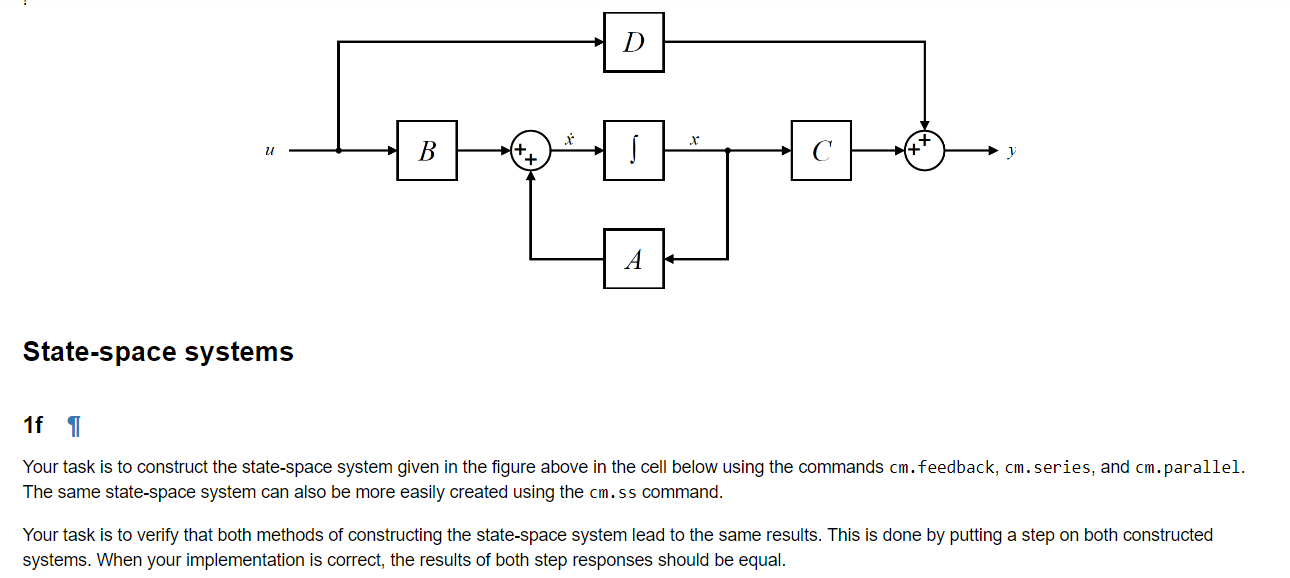
Your task is to construct the state-space system given in the figure above in the cell below using the commands cm. feedback, cm. series, and cm.parallel. The same state-space system can also be more easily created using the cm. ss command. Your task is to verify that both methods of constructing the state-space system lead to the same results. This is done by putting a step on both constructed systems. When your implementation is correct, the results of both step responses should be equal