the question is right above where it says function. it is mathlab coding

the question is to take this code (which is the naive gauss code) and implement gaussian elimination with partial pivoting. so just modify the code to gaussian elimination with partial pivoting.

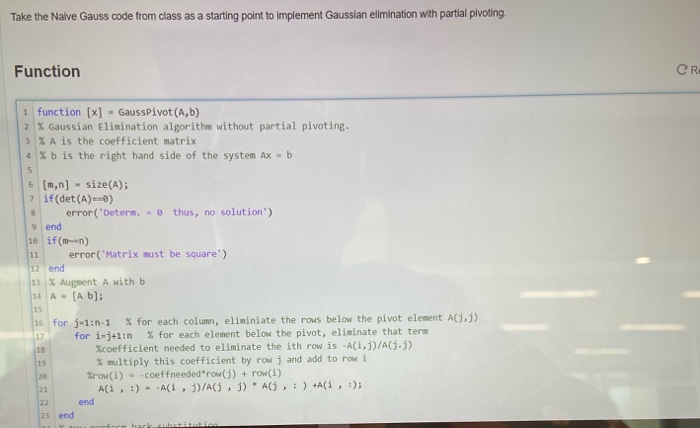
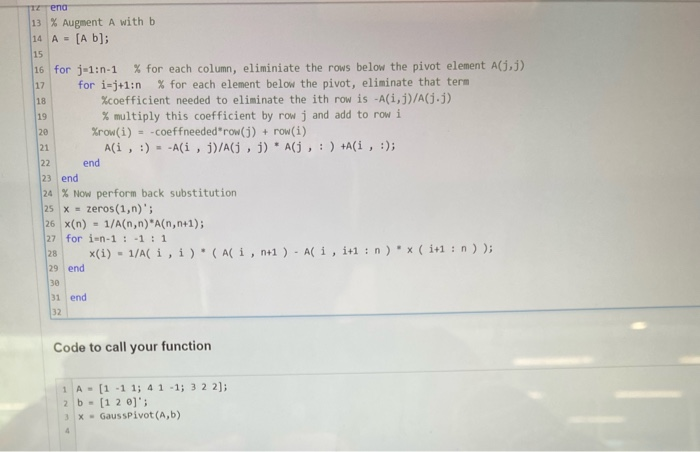
Take the Naive Gauss code from class as a starting point to implement Gaussian elimination with partial pivoting. Function CR 1 function [x] - Gauss Pivot (A,b) 7 % Gaussian Elimination algorithm without partial pivoting. 3 % A is the coefficient matrix 4 %b is the right hand side of the system Ax = b 6 (m,n) - size(A); 7 if(det(A)==) error('Detern. - thus, no solution') 9 end 10 if(men) error("Matrix must be square') 12 end 13 % Augment A with b 14 A - [A b]; 16 for j-1:n 1 % for each column, eliminiate the rows below the pivot element A(3) for i-j+1:0 % for each element below the pivot, eliminate that term Xcoefficient needed to eliminate the ith row is -A(i, j)/(1-) % multiply this coefficient by row j and add to row i Xrow(i) - coeffneeded"row() + row(i) Ali, :) - A(1, 1)/A , 1) A :) +Ali, :); end end end 13 % Augment A with b 14 A = [a b]; 16 for j-1:n-1 % for each column, eliminiate the rows below the pivot element A(1,1) for i=j+1:n % for each element below the pivot, eliminate that term %coefficient needed to eliminate the ith row is -A(i, j)/A(j.j) % multiply this coefficient by row j and add to row i Xrow(i) = -coeffneeded"row() + row(i) Ali, :) --A(i, j)/A(, j) * A(j, : ) +A(i , :); end 23 end 24 % Now perform back substitution 25 X = zeros (1,n)'; 26 x(n) = 1/A(n,n)*A(n,n+1); 27 for i-n-1:-1:1 28 (1) - 1/A i, i). (Ali, n+1 ) - Ali, i+1:n) x ( 1+1 : 0)); 29 end 31 end Code to call your function 1 A- [1 -1 1; 41 -1; 3 2 2]; 2 b = [1 2 ]; 3 X - GaussPivot (A,b)