Question: The recurrence T(n) = 2T(n - 2) + n describes the running time of algorithm A. A competing algorithm A' has a running time of

The recurrence T(n) = 2T(n - 2) + n describes the running time of algorithm A. A competing algorithm A' has a running time of T'(n)=16T'(n - b) + n. What is the smallest integer value for b such that A' is asymptotically faster than A?

Assume the same Case applies to both Algorithms. 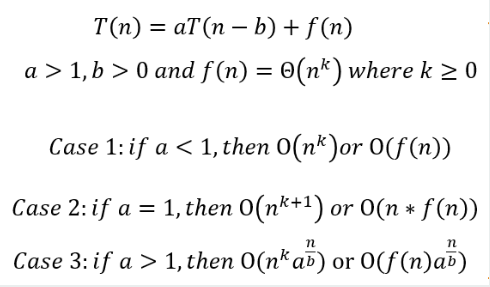The recurrence T(n) = 2T(n - 2) + n describes the running time of algorithm A. A competing algorithm A' has a running time of T'(n)=16T'(n - b) + n. What is the smallest integer value

T(n)=aT(nb)+f(n)a>1,b>0andf(n)=(nk)wherek0Case1:ifa1,thenO(nkabn)orO(f(n)abn) T(n)=aT(bn)+f(n)a1,b>1andf(n)=(nklogpn)Case1:iflogba>kthen(nlogba)Case2:iflogba=kifp>1,then(nklogp+1n)ifp=1,then(nkloglogn)ifp

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

1. What is the worst-case order of complexity for an algorithm that does the following: Finding the first occurrence of a given target in an integer array. Select one: a. O(n) b. O(log n) c. O(n log...

The recurrence T(n) = 7T(n/2)+n^(2) describes the running time of an algorithm ALG. A competing algorithm ALG' has a running time of T' (n) = aT' (n/4) + n 2 log n. What is the largest value of a...

The answer is given. Please explain in detail why a=99. The recurrence T(n) = 10T(n/3) + n2 describes the running time of an algorithm A. A competing algorithm A, has a running time of T'(n) =...

There is an algorithm for matrix multiplication that multiplies two nx n matrices by performing 7 recursive calls, each of which multiplies two n/2xn/2 matrices. The additional work performed during...

Question 15 2 pts What is the worst-case time complexity of the algorithm given below? CountValuesLessThanT Input: a1, a2.,. n, the length of the sequence. T, a target value. Output: The number of...

Suppose you have a problem in which the feature matrix, X, has 100 million rows and 200 columns. If each element of X is stored as a 64-bit double precision floating point number, how much memory is...

3. (3 pt) Consider the following recursive function that solves the Tower of Hanoi puzzle (https://www.mathsisfun.com/games/towerofhanoi.html). Note that n is the number of disks; from, to and...

Question 1: (20 Marks] There are two algorithms for a problem. The running time of Algorithm I is expressed as T(n) = 3T(n 2) + 0(1) and the running time of Algorithm II is expressed as T(n) = 3T...

1. Assume the addition of the two functions: public void recursiveDelete(int ky) { // calls the private version } private Node recursiveDelete(int ky, Node n); Write both functions. 2. Algorithm A...

(a) Suppose you are given two sets of n points, one set(p1,P2 .Pn} on the line y = 0 and the other set {Q1,Q2, . . . ,9a} on the line y = 1. Create a set of n line segments by connecting each point...

Distinguish between volume-based and operations- based cost drivers in the airline industry.

What amount of heat will be generated in the circuit shown in Fig. 3.31 after the switch Sw is shifted from position 1 to position 2? C Sw 62 6,

If the insured misrepresented his or her age on the insurance application, what is the result when the insured dies and his or her beneficiary seeks payment? The beneficiary will not receive payment...

Process 1 Process 2 T T2 In the two processes shown in the figure aside, the same amount of heat, Q, is supplied to equal amounts (in moles) of different gases, gas A and gas B. Both gases are...

LO1.8 (Appendix) Understand graphs, curves, and slopes as they relate to economics.

LO1.7 Explain how economic growth and international trade increase consumption possibilities.

LO1.6 Apply production possibilities analysis, increasing opportunity costs, and economic growth.