The Science of Term Structure Models

this is problem.

and this is example

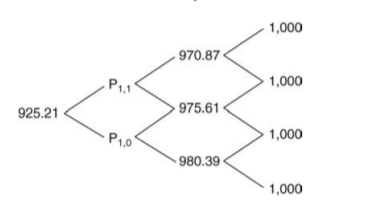
1. I don't really understand that question 7-2 states The experiences of 6-month, 1-year, and 1.5-year zeros are 97.5610, 95.0908, and 92.5069. Taking the picture above as an example, I understand that P1,1 P1,0, and 1-year are 970.87, 975.61, and 980.39, respectively. However, in this problem, 6-month, which was expected to have two values, came out as 97.5610, one value. 1-year, which was expected to have three values, also came out one value as 95.0908, and 1.5-year, which was expected to have four values, came out also one value as 92.5069.

Do I know something wrong?

2. Is it okay not to assume the Face value in question 7-2? 3. Please just solve the problem.

7.2 Assume that the true 6-month rate process starts at 5% and then increases or decreases by 100 basis points every 6 months. The probability of each increase or decrease is 50%. The prices of 6-month, 1-year, and 1.5-year zeros are 97.5610, 95.0908, and 92.5069. Find the risk-neutral probabilities for the six-month rate process over the next year (i.e., two steps for a total of three dates, including today). Assume, as in the text, that the risk-neutral probability of an up move from date 1 to date 2 is the same from both date 1 states. As a check to your work, write down the price trees for the 6-month, 1-year, and 1.5-year zeros. 1,000 970.87 P11 1,000 925.21 975.61 P10 1,000 980.39 1,000 7.2 Assume that the true 6-month rate process starts at 5% and then increases or decreases by 100 basis points every 6 months. The probability of each increase or decrease is 50%. The prices of 6-month, 1-year, and 1.5-year zeros are 97.5610, 95.0908, and 92.5069. Find the risk-neutral probabilities for the six-month rate process over the next year (i.e., two steps for a total of three dates, including today). Assume, as in the text, that the risk-neutral probability of an up move from date 1 to date 2 is the same from both date 1 states. As a check to your work, write down the price trees for the 6-month, 1-year, and 1.5-year zeros. 1,000 970.87 P11 1,000 925.21 975.61 P10 1,000 980.39 1,000