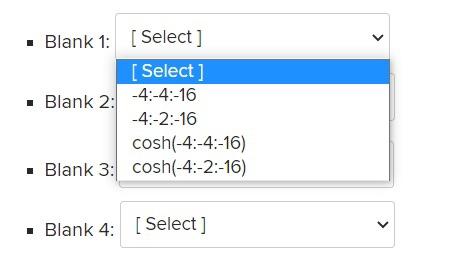
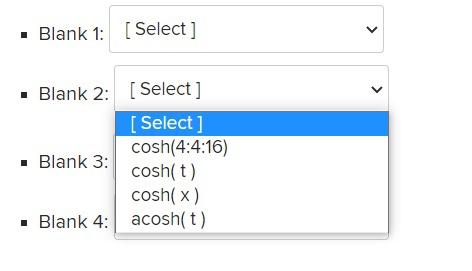
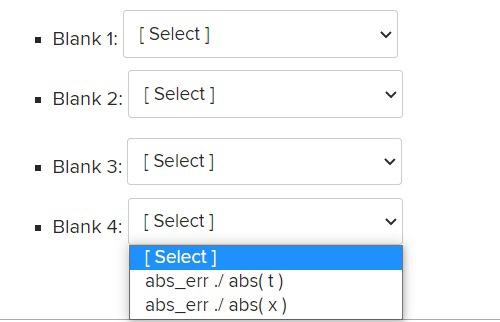
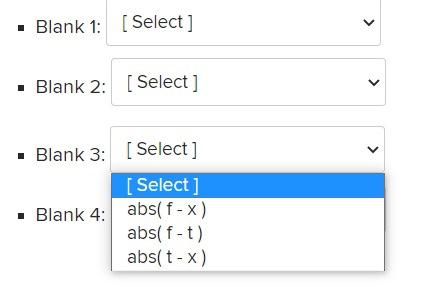
The script below computes the absolute and relative errors arising in numerically calculating the inverse of hyperbolic cosine acosh(x) using an alternate representation f(x) = log(x - x2 - 1) at x = cos(-4), cosh(-6), cosh(-8), cosh(-10), cosh(-12), cosh(-14), cosh(-16) . Fill in the blanks format long e t=... % blank 1 % blank 2 f = log(x-sqrt(x.^2-1)) abs_err = ... % blank 3 rel_err = % blank 3 disp( [x; abs_err; rel_err]') Choose the correct statement for each of the blank lines, Blank 1: [Select ] . Blank 2: Select ] . Blank 3: [Select] > Blank 4: [Select) Blank 1: [Select] [Select] Blank 2: -4:-4:-16 -4:-2:-16 cosh(-4:-4:-16) Blank 3: cosh(-4:-2:-16) > Blank 4: [Select] Blank 1: [Select ] > Blank 2: [Select ] [Select ] cosh(4:4:16) Blank 3: cosh(t) cosh(x) Blank 4: acosh(t) Blank 1: [ Select] Blank 3: [Select] Blank 3: [Select ] [Select ] Blank 4: abs(f-x) abs(ft) abs(t-x)