The Sensitivity Report is shown below. Here 1E+30 is an infinitely large positive number.

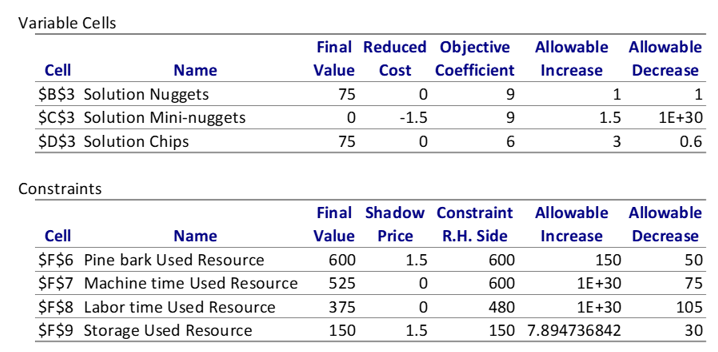
1. If the unit profit on nuggets increases to $9.5 and the unit profit on chips decreases to $5.6, will the optimal solution (values of x1, x2, and x3) change?

2. What is the additional profit one can get if the amount of pine bark increases from 600 pounds to 602?

3. If the unit profit on nuggets decreases to $8.5 and unit profit on mini-nuggets decreases to $8, what is the total profit if the optimal (solution) quantities (x1, x2, and x3) are applied?

4. The firm can obtain an additional 100 pounds of pine bark at the cost of $2/pound. Do you recommend the firm to obtain the additional 100 pounds of pine bark?

1.

Variable Cells Cell Name $B$3 Solution Nuggets $C$3 Solution Mini-nuggets $D$3 Solution Chips Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 75 0 9 1 1 0 -1.5 9 1.5 1E+30 75 0 6 3 0.6 Constraints Cell Name $F$6 Pine bark Used Resource $F$7 Machine time Used Resource $F$8 Labor time Used Resource $F$9 Storage Used Resource Final Shadow Constraint Allowable Allowable Value Price R.H. Side Increase Decrease 600 1.5 600 150 50 525 0 600 1E+30 375 0 480 1E+30 105 150 1.5 150 7.894736842 75 30