There are many greedy algorithms that can find a minimum-cost spanning tree (MST) for a graph 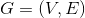with edge costs 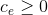for each edge 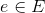. After computing an MST 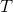for graph 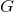, you realize that the cost you used for one of the edges was too high. Specifically, some edge 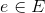has real cost 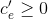that is strictly less than 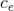, which is the cost of the edge you just used.

You could use 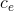instead and run the algorithm, but suppose this happens frequently. Could you take advantage of the fact that we know what the MST looks like for almost the right set of edge costs? Construct an MST 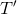by using 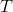for the correct set of edge costs. Make sure the run time is 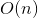. Prove the algorithm works and explain the run time.

G= (V, E) T G= (V, E) T