There are many questions contain which one is not correct

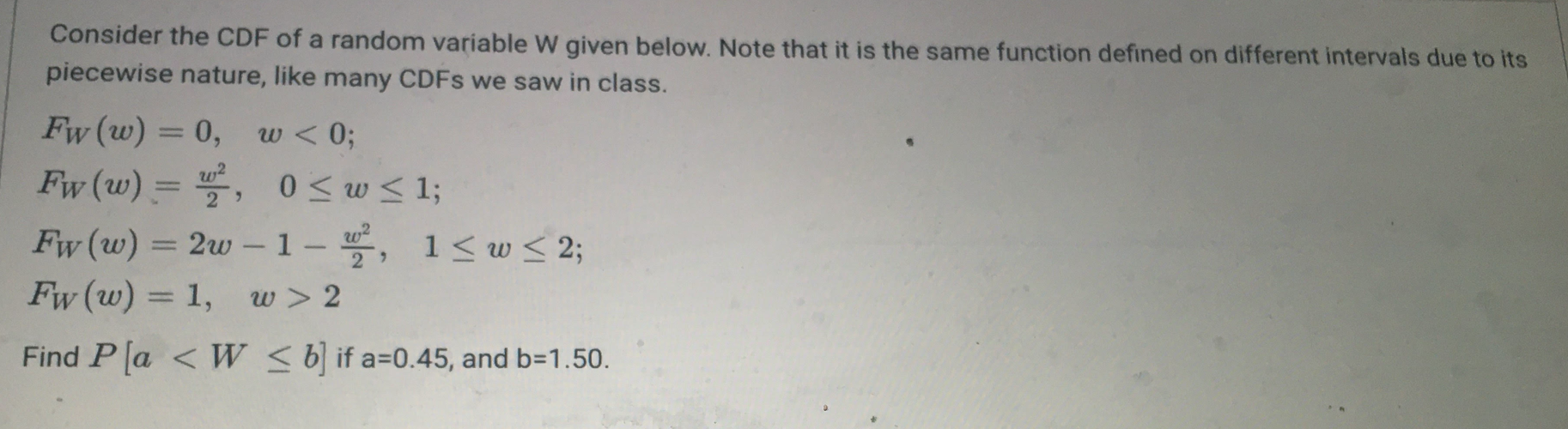
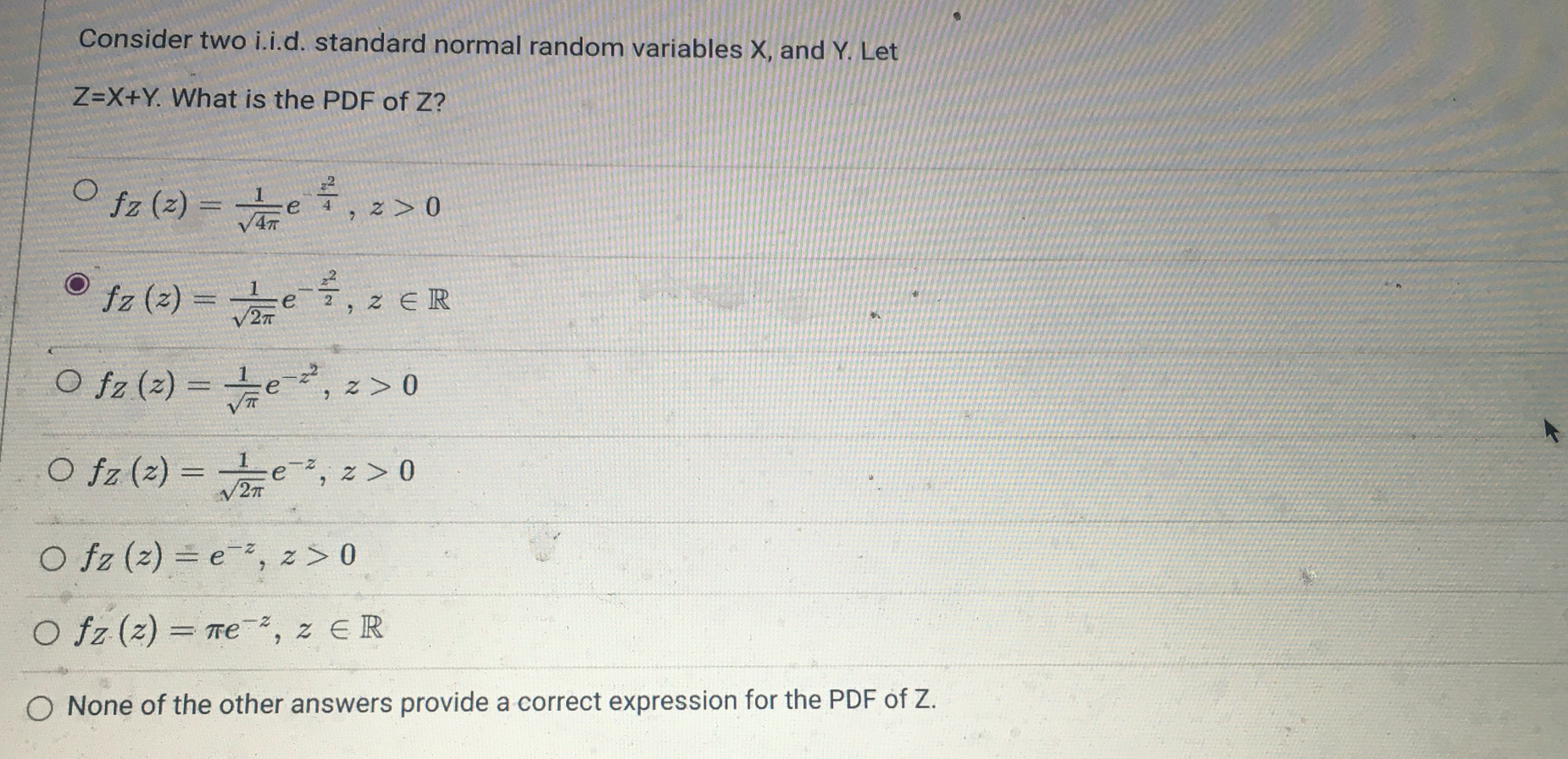
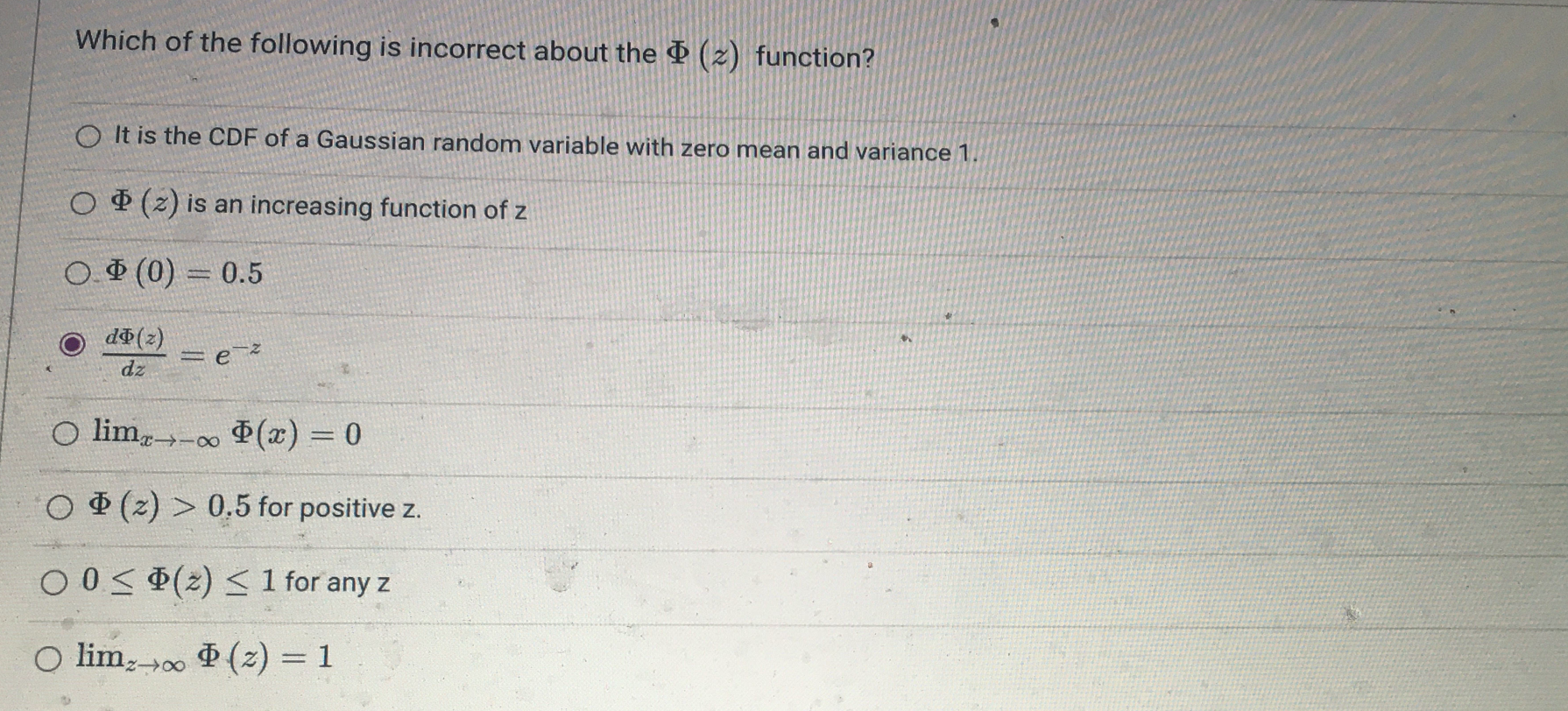
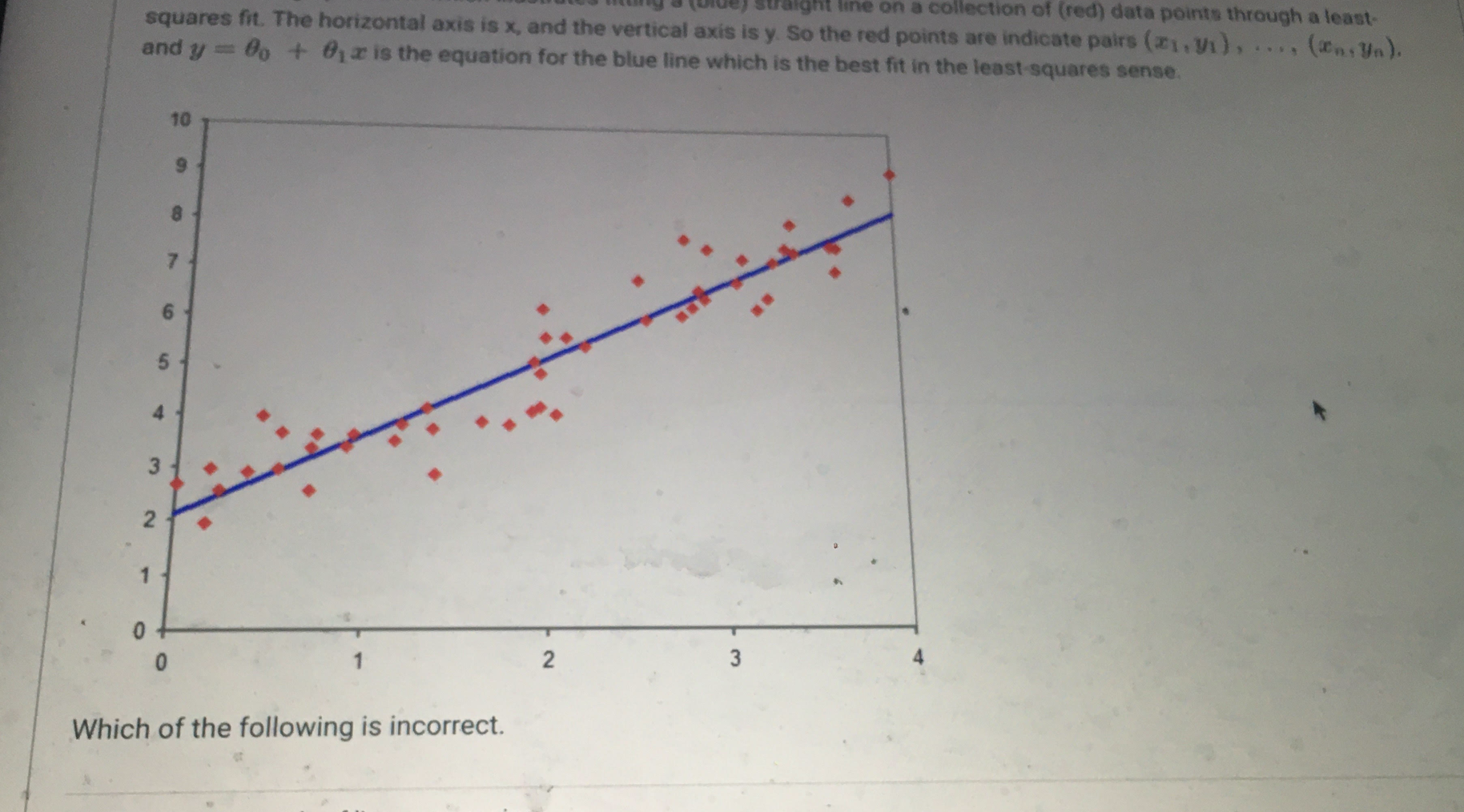
Consider the CDF of a random variable W given below. Note that it is the same function defined on different intervals due to its piecewise nature, like many CDFs we saw in class. FW (w) = 0, w 2 Find Pla 0 Ofz ( 2 ) = he z, z ER Ofz ( 2 ) = he z , 2>0 O fz ( 2 ) = -- ez, z>0 Ofz ( z ) = e-z, z>0 Ofz ( z) = Te z, z ER O None of the other answers provide a correct expression for the PDF of Z.Which of the following is incorrect about the $ (2) function? It is the CDF of a Gaussian random variable with zero mean and variance 1. O ( 2) is an increasing function of z O. $ (0) = 0.5 O do(z) =ez dz O limz-- (x) = 0 O D (z) > 0.5 for positive z. O0 0 Instead of using the sums of squares of the residuals as a performance metric, one can simply use the sum of the residuals without squaring. The resulting best line will be guaranteed to be close to all the points. This problem can be formulated as a maximum likelihood parameter estimation problem in the presence of additive white Gaussian noise. O 01 >0 O. If a new point (In+1, Un+1 ) is added to the list, and the blue line is recomputed with the extra point, this would not change the new least squares fit with the additional point, as long as Un+1 = 0 + 01X2+1. O The best line that fits those points in the least-squares sense is obtained by finding the line that minimizes the sum of squares of the residuals from the line to the points