This is an calculus optimization type question.

Both the QUESTION and SOLUTION are shown below.

My first query relates to the statement

1. "strictly greater than M for all M > 0"

The statement is underlined in RED below.

Please show how, in more detail, it can be argued that "this", is greater than M for all M >0

For example, is it possible to say

Mlim(2M210M+25)

since the limit of a polynomial, whose leading coefficient is positive, is infinity.

2. My next query relates to

(M8,M,0)=M264+M2+0>M2M

which is underlined in BLUE below. Please explain the logic/reasoning for this ?

3. My final query relates to all text underlined in GREEN. Explain how

25=(x+y+z)2

is determined and also explain how

(x,y,z)=9

is determined.

Explain the conclusion underlined in GREEN (That is, our constraint set D lies on the 3-sphere .....)

Please explain clearly showing each step as thoroughly as possible. If you are using hand written notes, then please ensure they are neat and legible, as it is difficult to interpret illegible hand-written notes. Alternatively, use LaTex.

QUESTION

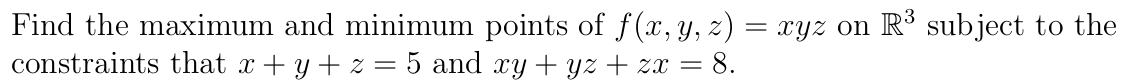
Find the maximum and minimum points of f (:13, y, z) = xyz on R3 subject to the constraints that :1: + y + z = 5 and my + yz + 2x = 8. First, let us put this into standard form {3%, f (3:, y) = rcyz. st. g1(:r,y,z) =x+y+z5=0, 92(xiy1z) =my+yz+zar8=D. Thus, our domain is D: {(17,152)ER3|$+y+z=5}{(m,y,z) ER3|$y+yz+zm=8}. \\,_I '-v" D1 D2 Let us now apply our cookbook procedure. 1. f is continuum on D. By inspection we can see that (1,2,2) is a point in D which is thus non-empty. Furthermore, we can argue that D is closed in the following way: it is the intersection of two sets 201 and D2, which are dened in terms of continuous functions and equality constraints, and are thus closed themselves. However '13] is not bounded since, for any M > 0, then (5 M, M,0} E 131 while: ||(5M,M,0)|| ={5 M)2+M2+0 =2M2 10M+25. There are a number of ways to argue that this is strict]! greater than M for all M > 0 [try to come up with one). Nor is D2 bounded since, for any M > 0, then (EB/M, M, 0) E D2 while: _ = > . |(M,M,0)|| M2+M +0>M _M Since neither 01 nor I12 are bounded, we cannot immediately conclude that their intersection D is, and hence compact. However, note that D2 appears to be dened in terms of cross-product terms. So let's consider an arbitrary point (:5, y, z) E D. Then (3:, y, 2) 6 D1 so 5: + y + z = 5 i.e. 25={:r+y+z)2 =x2+y2+zz+2$y+2yz+22$ =$2+y2+22+2(:y+yz+z:r). Since (:Iz,y,z) E 'D then (at,y,z) E D2 and xy+yz+z1r =8. So: 25=$2+y2+22+2-8=$2+y2+22+16. Thus, for all (:r,y, z) E D, we have ||(1:,y,z)|| = 9. That is: our constraint set D lies on the 3-5 here of centre 0 0 U and radius 3. So D is bounded b sa an M > 3. By Weierstrass\" Theorem, our problem has both a maximum and minimum