This is for CS101 class. If you answer the questions accordingly, I would be glad. Thank you in advance.

Introduction

As programs get longer, managing them becomes increasingly difficult. That's where methods come in handy. In essence, a method is just a named collection of statements. Once declared, a method can be invoked any number of times. This lab will give you practice creating and using (static) methods.

Documenting your code

You can do this assignment in a single project within your lab06 workspace.

Design, implement and test the following simple methods, all of which can be in the same class as your main method

- write a method called power that computes and returns x to the power y, where x is any real value & y is a positive integer. Use repeated multiplication, not Math class methods..

- write a method to compute n factorial, where n is a positive integer. Use a for loop that decrements its loop-control-variable each time. Return a int result.

- write a method reverse that takes a String parameter, s, and returns a String that is the reverse of s. For example, if s is "abcd", the method should return "dcba".

- write a method with the signature "public static int toDecimal( String base2)" that converts the given base2 String to its decimal --base10-- equivalent, as an int. For example, if base2 is "110", it should return 6, whereas if it was "1011", it should return 11. You should be able to do this without using Math class methods, and without computing the power of the most significant digit.

- write a method that converts a positive decimal int value into the corresponding binary String.

Demonstrate your methods by doing the following:

- print a table with columns n, n-squared, n-cubed & n to the power 4, for values of n from -1 to 10 inclusive

- print a table of n and n-factorial, for values of n from 1 to 15

- read two binary (base-2) Strings from the user, convert them to decimal, then add them together and print the result in binary form.

- read a line of text from the user and output it again, but with each word reversed. For instance, were the user to enter "gnimmargorP si nuf", your program should output "Programming is fun".

- print a table that shows the "raw" calculations for the Taylor series expansion of sin(x), where x is read from the user. Your table should have columns for the term number n, and for (-1)^n, x^(2n+1), (2n+1)!, the term itself computed from these values, and the sum of the preceding terms with this one, i.e. the current approximation to sin(x). The term number n should go from 0 up to, say, 10.

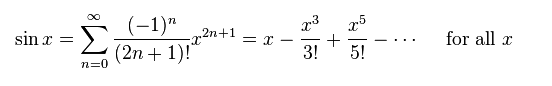
- obviously computing sin(x) like this results in significant errors and is very inefficient! A better approach is to compute each term from the previous one (hint: think how can you compute x^5/5! from x^3/3! ). Implement sin(x) as a method using this approach and test it by comparing its answers with those from Math.sin(x).

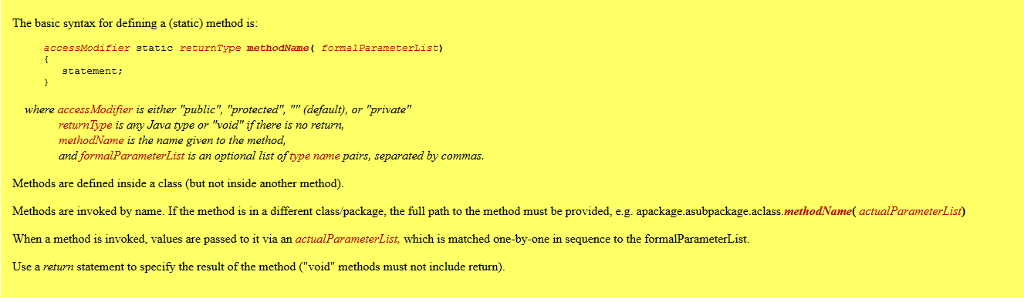
The basic syntax for defining a (static) method is: accessModifier static returnType methodName( formalParameterList) gtatement where access.Modifier is either "public" "protected", "" (default), or "private" returnTipe is ary Java type or "void" if there is no return, methodName is the name given to the method, and formalParameterList is an optional list of ope name pairs, separated by commas Methods are defined inside a class (but not inside another method) Methods are invoked by name. If the method is in a different class/package, the full path to the method must be provided, e.g. apackage.asubpackage.aclass.methodNamel actualParameterList) When a method is invoked, values are passed to it via an actualParameterList, which is matched one-by-one in sequence to the formalParameterList. Use a return statement to specify the result of the method ("void" methods must not include return)