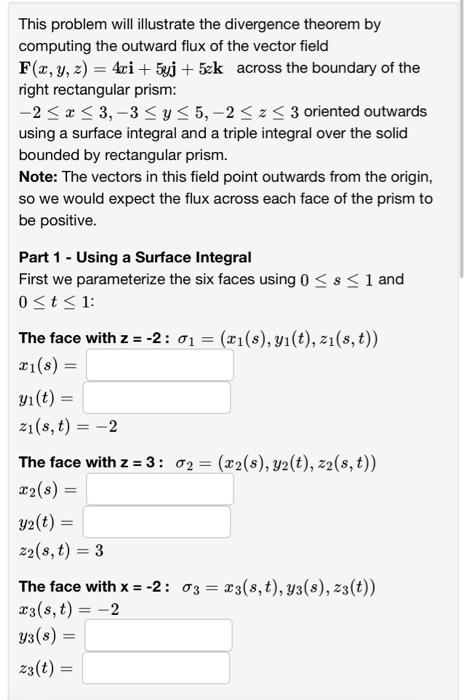
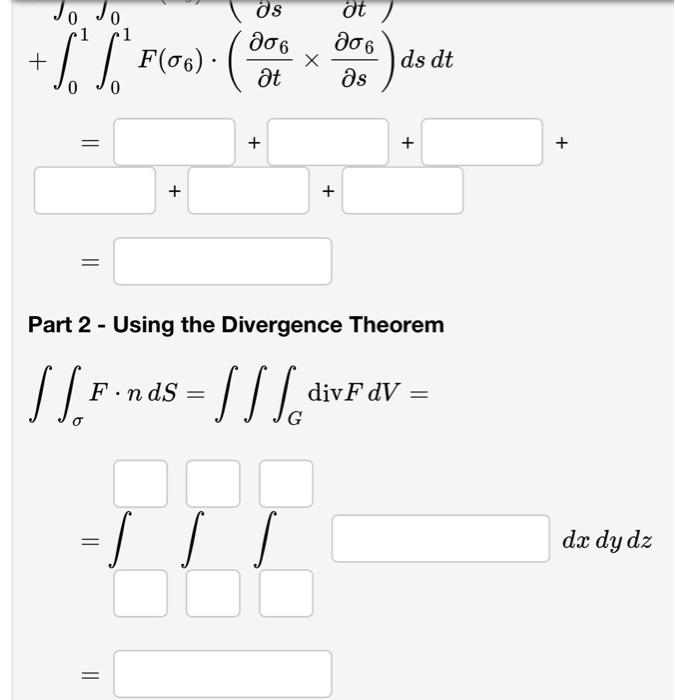
This problem will illustrate the divergence theorem by computing the outward flux of the vector field F(x, y, 2) = 4ri + 5yj +50k across the boundary of the right rectangular prism: -2 x 3,-3 y 5,-2 z 3 oriented outwards using a surface integral and a triple integral over the solid bounded by rectangular prism. Note: The vectors in this field point outwards from the origin, so we would expect the flux across each face of the prism to be positive. Part 1 - Using a Surface Integral First we parameterize the six faces using 0 s 1 and 0 t 1: The face with z = -2: 0 = (x(s), y(t), z(s, t)) *1(s) = y(t) = z1(s, t) -2 The face with z = 3: 02 = (x2(8), y2(t), z2(s, t)) x2 (s) = y2(t) = z2(s, t) = 3 The face with x = -2:03 = 23(s, t), y3(8), z3(t)) 23(s, t) = -2 y3(s) = z3(t) = The face with x = 3: 04 (4(s, t), y4(8), 24(t)) = 24 (s, t) = 3 Y4 (8) = z4(t) = The face with y = -3: 05 = x5 (8) = y5(s, t) =-3 25 (t) = The face with y = 5: 06 = = (x6(3), y6(s, t), 26(t)) 26 (8) = y6 (s, t) = 5 z6(t) = = (r5(s), ys(s, t), 25(t)) Then (mind the orientation) X [F.nds = [["" F(0) - (30 + S S F (0) ( 202 ds dt 802 t 0 0 803 t s 804 s 805 + S S F (03). 0 + S S F (0). ( 0 0 + 0 0 + S S P (0). ( + S S F (06). ( 0 II X X X X 20 t 205 t 806 806 X t s + ds dt ds dt ds dt ds dt 301) ds d + ds 1 206 [ [ F (06). (20 t 0 0 = So || + F.ndS= n d + = dt 206 s Part 2 - Using the Divergence Theorem [[ = [ /[di G =[ ] , , + ds dt + divF dV = + dx dy dz