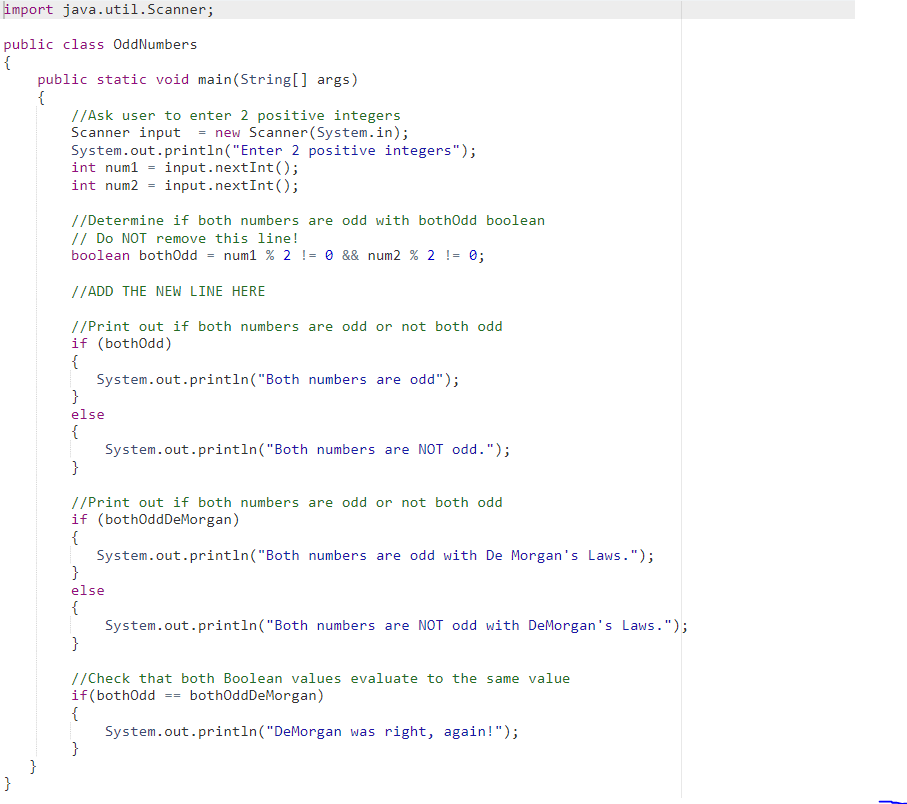
This program reads input from the user to determine if the user's two numbers are BOTH odd. The program computes 2 boolean expressions in order to determine if the equivalent De Morgan expression gives the same result when checking for odd numbers. This expression is given in the code: boolean bothOdd = num1 % 2 != 0 && num2 % 2 != 0; Convert the bothOdd Boolean into its equivalent De Morgan style boolean expression on its own line and call it bothOddDeMorgan. De Morgan's Laws show equivalencies, so you can work Boolean expressions in EITHER direction, not just with distributing the ! throughout an expression! Your resulting boolean expression for bothodd De Morgan should produce the same result as bothodd. The resulting program should still be able to successfully determine if two numbers entered by a user are both odd or not. import java.util.Scanner; public class OddNumbers { public static void main(String[] args) { //Ask user to enter 2 positive integers Scanner input = new Scanner(System.in); System.out.println("Enter 2 positive integers"); int num1 = input.nextInt(); int num2 = input.nextInt(); //Determine if both numbers are odd with bothOdd boolean // DO NOT remove this line! boolean bothOdd = num1 % 2 != 0 && num2 % 2 != 0; //ADD THE NEW LINE HERE //Print out if both numbers are odd or not both odd if (bothOdd) { System.out.println("Both numbers are odd"); } else { System.out.println("Both numbers are NOT odd."); } //Print out if both numbers are odd or not both odd if (bothOddDeMorgan) { System.out.println("Both numbers are odd with De Morgan's Laws."); } else { System.out.println("Both numbers are NOT odd with DeMorgan's Laws."); } //Check that both Boolean values evaluate to the same value if (bothOdd == bothOddDeMorgan) { System.out.println("DeMorgan was right, again!"); } } } This program reads input from the user to determine if the user can ride the rollercoasters and swim in the pools at the amusement park. The program computes 2 boolean expressions in order to determine what the user is allowed to do: boolean cannotRide = !(oldEnough && tallEnough); and boolean cannotSwim = !(canSwim || hasLifeJacket); Convert these two lines into their equivalent De Morgan style boolean expressions. Negate the AND in the first statement and negate the OR in the second statement using De Morgan's Laws. Your resulting boolean expression for cannotRide should include both oldEnough and tallEnough. Your resulting boolean expression for cannotSwim should include both can Swim and hasLife Jacket. The resulting program should still be able to successfully determine if the user can ride the rides and swim in the pool. import java.util.Scanner; public class Amusement Park { int age = static int AGE_LIMIT = 12; static int HEIGHT_LIMIT = 48; public static void main(String[] args) { Scanner input = new Scanner(System.in); System.out.println("Enter your age: "); input.nextInt(); System.out.println("Enter your height in inches: "); int height = input.nextInt(); boolean oldEnough = age >= AGE_LIMIT; boolean tallEnough = height >= HEIGHT_LIMIT; // CHANGE THIS LINE // Convert this boolean expression into its De Morgan equivalent boolean cannotRide = ! (oldEnough && tallEnough); if (cannotRide) { System.out.println("You may not ride the rollercoasters."); } else { System.out.println("You may ride the rollercoasters!"); } System.out.println("Can you swim? Enter true or false."); boolean canSwim = input.nextBoolean(); System.out.println("Do you have a life jacket? Enter true or false."); boolean hasLifeJacket = input.nextBoolean(); // CHANGE THIS LINE 1/ Convert this boolean expression into its De Morgan equivalent boolean cannotSwim = !(canSwim || hasLifeJacket); if (cannotSwim) { System.out.println("You may not swim in the pool."); } else { System.out.println("You may swim in the pool!"); } } }