This project will use the logistic map:

F(x) = rx(1-x), where x is an element in [0, 1] and r > 0,

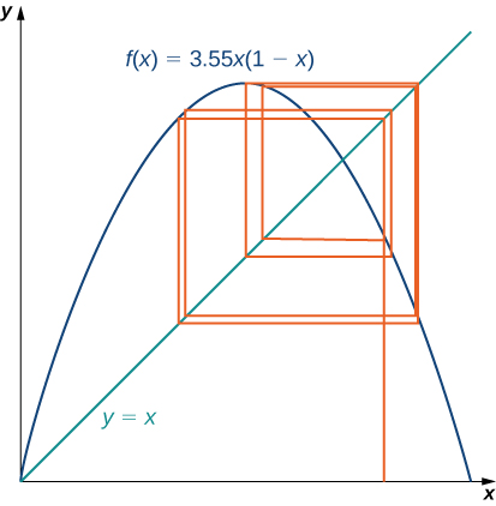
is the function in our iterative process. The logistic map is a deceptively simple function; but, depending on the value of r, the resulting iterative process displays some very interesting behavior. It can lead to fixed points, cycles, and even chaos. To visualize the long-term behavior of the iterative process associated with the logistic map, we will use a tool called a cobweb diagram. As we did with the iterative process we examined earlier in this section, we first draw a vertical line from the point (x0, 0) to the point (x0, f(x0))=(x0, x1), and continue the process until the long-term behavior of the system becomes apparent. The figure below shows the long-term behavior of the logistic map when r= 3.55 and x0=0.2. (The first 100 iterations are not plotted.) The long-term behavior of this iterative process is an 8-cycle.

1. Let r= 0.5 and choose x0=0.2. Using a spreadsheet (Excel or Google Sheets) that calculates the formula for you, calculate the first 10 values in the sequence. Insert the spreadsheet table below.
2. 1. State the formula entered into the spreadsheet:
   2. Does the sequence appear to:
      1. Converge? If so, to what value?
      2. Result in a cycle? If so, what is the period of the cycle?
   3. Insert spreadsheet table.

. f(x) = 3.55x(1 - x) y = X