This questions is in scala

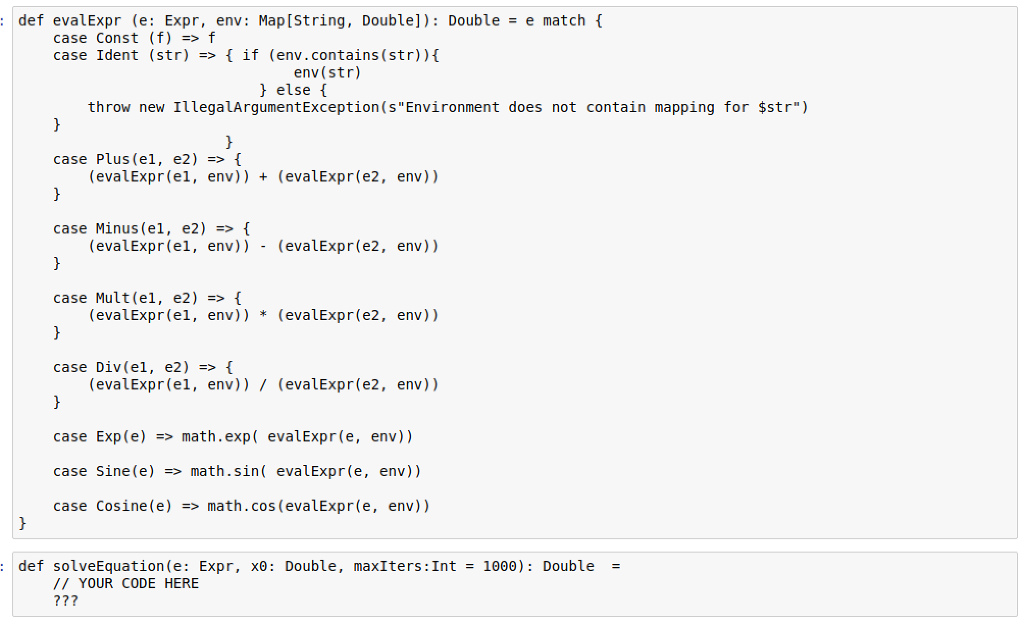
2B: Newton's Algorithm Reloaded (10 points) Let's revisit problem 5 from assignment 1. Back in assignment 1, we hard coded the expression and its derivative. Here, we will use our Expr abstract syntax to define expressions and use the function you wrote in 2A to compute derivatives. You may also use the evalExpr function provided below. Newton invented the Newton-Raphson method for solving an equation. We are going to ask you to write some code to solve equations solveEquation(e: Expr, x0: Double, maxIters: Int-1000) Assume that the input expression has involves just one variable "x". To solve an equation of the form x2 - 3x 20 with initial guess at the solution: say xo = 4.5 we will input vai e- Plus(Minus (Mult(Ident ("x"), Ident ("")), Mult(Const(3.0), Ident("x"))), Const(2.0) ) into the function solveEquation( e, 1.5, 1000) Each time we have the ith guess x, we update it as f(xi) f (x) For our equation, f(x) = x2-3x + 2 and f,(x) = 2-3 (f, is the derivative off. Thus, our update equation is - 3x +2 2x,-3 2B: Newton's Algorithm Reloaded (10 points) Let's revisit problem 5 from assignment 1. Back in assignment 1, we hard coded the expression and its derivative. Here, we will use our Expr abstract syntax to define expressions and use the function you wrote in 2A to compute derivatives. You may also use the evalExpr function provided below. Newton invented the Newton-Raphson method for solving an equation. We are going to ask you to write some code to solve equations solveEquation(e: Expr, x0: Double, maxIters: Int-1000) Assume that the input expression has involves just one variable "x". To solve an equation of the form x2 - 3x 20 with initial guess at the solution: say xo = 4.5 we will input vai e- Plus(Minus (Mult(Ident ("x"), Ident ("")), Mult(Const(3.0), Ident("x"))), Const(2.0) ) into the function solveEquation( e, 1.5, 1000) Each time we have the ith guess x, we update it as f(xi) f (x) For our equation, f(x) = x2-3x + 2 and f,(x) = 2-3 (f, is the derivative off. Thus, our update equation is - 3x +2 2x,-3