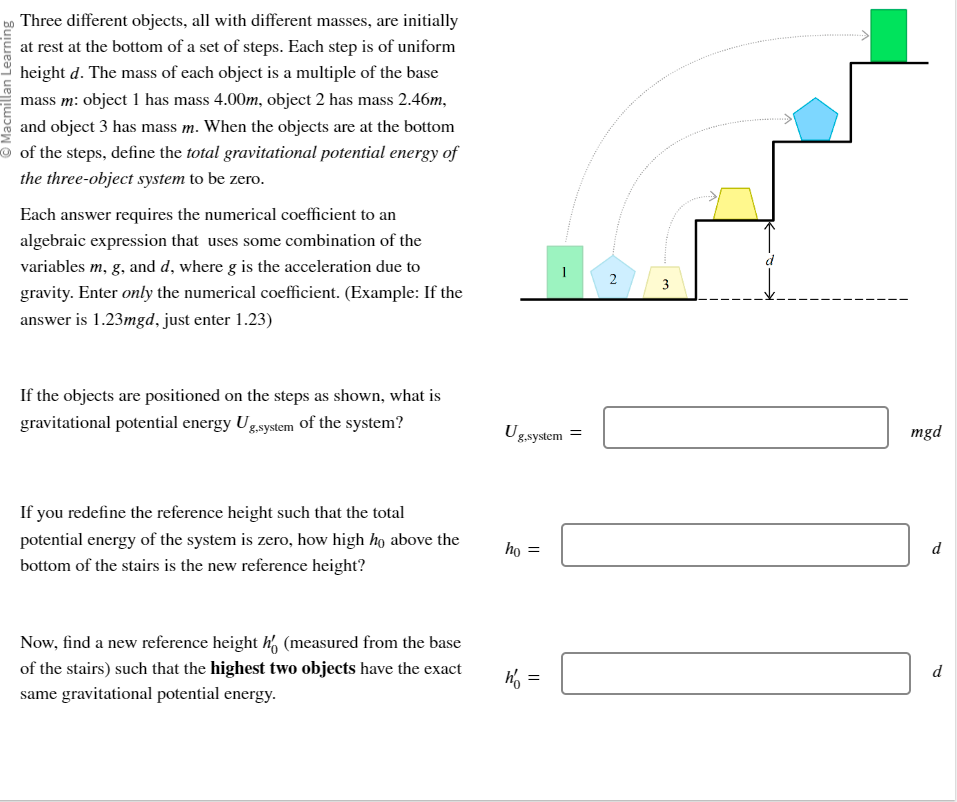
Three different objects, all with different masses, are initially at rest at the bottom of a set of steps. Each step is of uniform height d. The mass of each object is a multiple of the base mass m: object 1 has mass 4.00m, object 2 has mass 2.46m, and object 3 has mass m. When the objects are at the bottom of the steps, define the total gravitational potential energy of the three-object system to be zero. Each answer requires the numerical coefficient to an algebraic expression that uses some combination of the variables m, g, and d, where g is the acceleration due to 2 gravity. Enter only the numerical coefficient. (Example: If the 3 answer is 1.23mgd, just enter 1.23) If the objects are positioned on the steps as shown, what is gravitational potential energy U g system of the system? U g.system = mgd If you redefine the reference height such that the total potential energy of the system is zero, how high ho above the ho = d bottom of the stairs is the new reference height? Now, find a new reference height ho (measured from the base of the stairs) such that the highest two objects have the exact ho = same gravitational potential energy