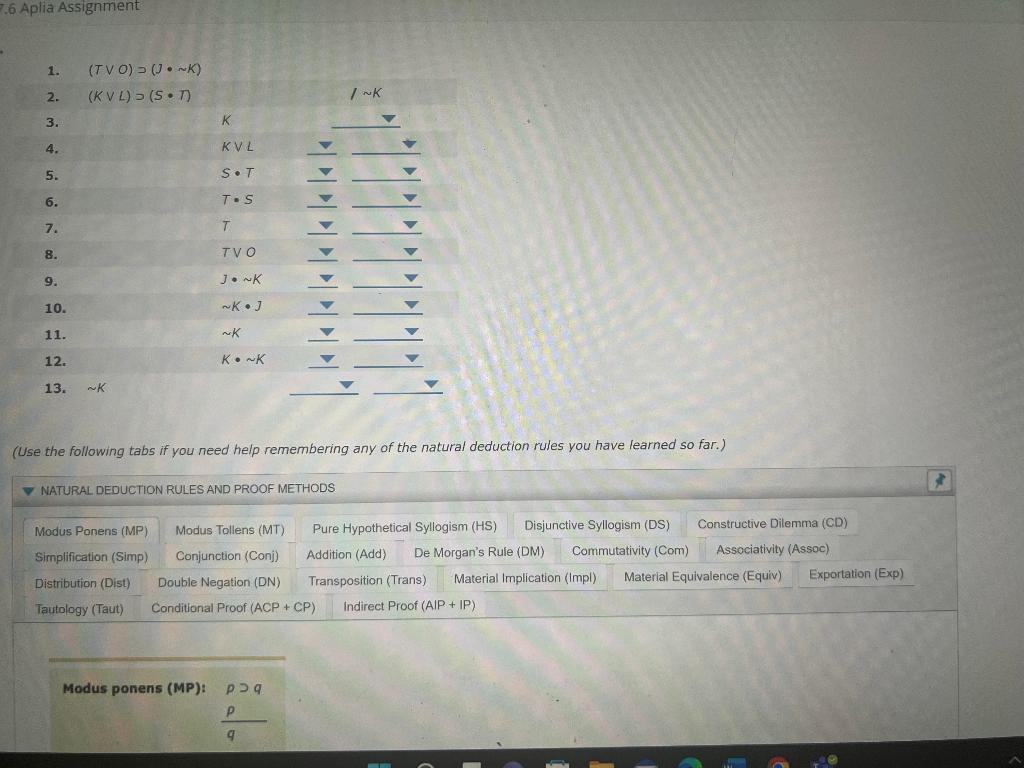
Question: To use the indirect proof method, begin by assuming the opposite of the proposition you need to prove on a new indented line as an
To use the indirect proof method, begin by assuming the opposite of the proposition you need to prove on a new indented line as an assumption for indirect proof (AIP). Then show that this assumption leads to a contradiction by deriving an explicit contradiction (which is a substitution instance of the form p ~p) within the scope of the indented sequence. Since the assumption implies a contradiction, it follows that the assumption must be false. Therefore, you can discharge the indented indirect proof sequence to obtain the negation of the AIP assumption, placing it on a non-indented line. The conclusion of the indirect proof sequence is justified by "IP" (indirect proof) and the line numbers from the entire indented sequence.
Like the conditional proof method, the indirect proof method can be used within the scope of another indented conditional or indirect proof sequence, and it can be used as a part of a larger proof to obtain a proposition that you need in order to perform a subsequent proof step. Remember that you cannot cite any line from within an indented sequence that has already been discharged as justification for any subsequent line.
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


